已知椭圆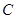 :
: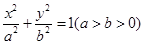 经过点
经过点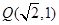 ,且焦点与双曲线
,且焦点与双曲线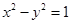 的焦点相同.
的焦点相同.
(Ⅰ)求椭圆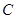 的方程;
的方程;
(Ⅱ)若过点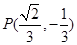 而不过点
而不过点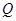 的动直线
的动直线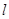 交椭圆
交椭圆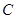 于
于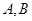 两点,证明:
两点,证明: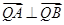 .
.
(本小题满分12分)下图是为了计算 的值而设计的程序框图,
的值而设计的程序框图,
(Ⅰ)将(1)、(2)两处缺失的语句补上。
(Ⅱ)指出程序框图中用的是那一种类型的循环结构,并用另一种循环结构画出程序框图。
(本小题满分10分)若二进制数100 011和八进制数
011和八进制数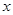 03相等,求
03相等,求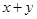 的值。
的值。
(本小题满分12分)已知函数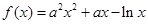 .
.
(1)当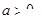 时,求函数
时,求函数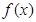 的单调区间;
的单调区间;
(2)设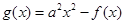 ,且函数
,且函数 在点
在点 处的切线为
处的切线为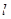 ,直线
,直线 //
//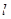 ,且
,且 在
在 轴上的截距为1.求证:无论
轴上的截距为1.求证:无论 取任何实数,函数
取任何实数,函数 的图象恒在直线
的图象恒在直线 的下方.
的下方.
(本小题满分12分)将一个半径适当的小球放入如图所示的容器最上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物 次,最后落入
次,最后落入 袋或
袋或 袋中.已知小球每次遇到障碍物时,向左、右两边下落的概率分别是
袋中.已知小球每次遇到障碍物时,向左、右两边下落的概率分别是

(1)分别求出小球落入 袋和
袋和 袋中的概率;
袋中的概率;
(2)在容器的入口处依次放入 个小球,记
个小球,记 为落入
为落入 袋中的小球个数,求
袋中的小球个数,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)在数列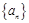 中,
中,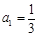 ,且
,且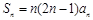 ,
,
(1)求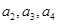 的值;
的值;
(2)归纳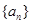 的通项公式,并用数学归纳法证明.
的通项公式,并用数学归纳法证明.