如图,已知椭圆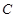 :
: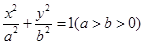 的离心率为
的离心率为 ,以椭圆
,以椭圆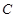 的左顶点
的左顶点 为圆心作圆
为圆心作圆 :
: ,设圆
,设圆 与椭圆
与椭圆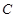 交于点
交于点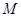 与点
与点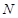 .(12分)
.(12分)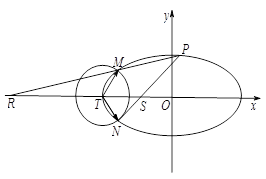
(1)求椭圆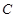 的方程;
的方程;
(2)求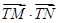 的最小值,并求此时圆
的最小值,并求此时圆 的方程;
的方程;
(3)设点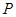 是椭圆
是椭圆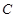 上异于
上异于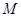 ,
,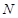 的任意一点,且直线
的任意一点,且直线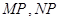 分别与
分别与 轴交于点
轴交于点 ,
, 为坐标原点,求证:
为坐标原点,求证: 为定值.
为定值.
(1)求动点 的轨迹
的轨迹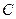 的方程;
的方程;
(2)已知圆 过定点
过定点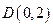 ,圆心
,圆心 在轨迹
在轨迹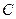 上运动,且圆
上运动,且圆 与
与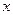 轴交于
轴交于 、
、 两点,设
两点,设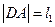 ,
,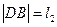 ,求
,求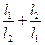 的最大值.
的最大值.
(1)求曲线E的方程;
(2)若过定点F(0,2)的直线交曲线E于G、H不同的两点,求此直线斜率的取值范围;
(3)若点G在点F、H之间,且满足 的取值范围。
的取值范围。
(1)求证:平面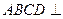 平面
平面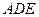 ;
;
(2)求正方形的边长;
(3)求二面角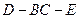 的平面角的正切值.
的平面角的正切值.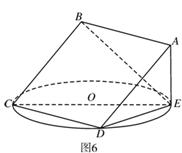
已知点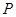 是⊙
是⊙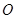 :
: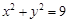 上的任意一点,过
上的任意一点,过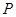 作
作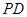 垂直
垂直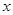 轴于
轴于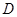 ,动点
,动点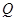 满足
满足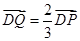 。
。
(1)求动点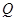 的轨迹方程;
的轨迹方程;
(2)已知点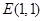 ,在动点
,在动点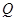 的轨迹上是否存在两个不重合的两点
的轨迹上是否存在两个不重合的两点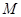 、
、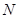 ,使
,使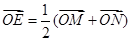 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线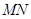 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
直线 经过两条直线
经过两条直线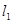 :
: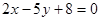 和
和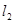
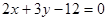 的交点,且分这两条直线与
的交点,且分这两条直线与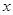 轴围成的三角形面积为
轴围成的三角形面积为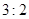 两部分,求直线
两部分,求直线 的一般式方程。
的一般式方程。