某工厂某种产品的年固定成本为250万元,每生产 千件,需另投入成本为
千件,需另投入成本为 ,当年产量不足80千件时,
,当年产量不足80千件时, (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时, (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润 (万元)关于年产量
(万元)关于年产量 (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
函数 ,曲线
,曲线 上点
上点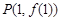 处的切线方程为
处的切线方程为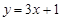
(1)若 在
在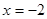 时有极值,求函数
时有极值,求函数 在
在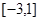 上的最大值;
上的最大值;
(2)若函数 在区间
在区间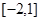 上单调递增,求
上单调递增,求 的取值范围.
的取值范围.
已知 满足不等式
满足不等式 ,求函数
,求函数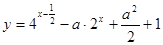 的最小值.
的最小值.
已知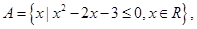

(1)若 ,求实数
,求实数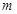 的值;
的值;
(2)若
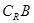 ,求实数
,求实数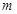 的取值范围.
的取值范围.
已知函数 ,其中
,其中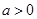 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若直线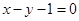 是曲线
是曲线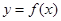 的切线,求实数
的切线,求实数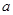 的值;
的值;
(3)设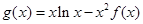 ,求
,求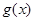 在区间
在区间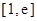 上的最大值.(其中
上的最大值.(其中 为自然对数的底数)
为自然对数的底数)
已知一个口袋中装有 个红球(
个红球(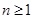 且
且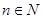 )和
)和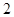 个白球,从中有放回地连续摸三次,每次摸出两个球,若两个球颜色不同则为中奖,否则不中奖.
个白球,从中有放回地连续摸三次,每次摸出两个球,若两个球颜色不同则为中奖,否则不中奖.
(1)当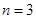 时,设三次摸球中(每次摸球后放回)中奖的次数为
时,设三次摸球中(每次摸球后放回)中奖的次数为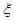 ,求的
,求的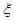 分布列;
分布列;
(2)记三次摸球中(每次摸球后放回)恰有两次中奖的概率为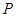 ,当
,当 取多少时,
取多少时,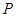 最大.
最大.