某旅游推介活动晚会进行嘉宾现场抽奖活动,抽奖规则是:抽奖盒中装有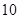 个大小相同的小球,分别印有“多彩十艺节”和“美丽泉城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球,若抽到两个球都印有“多彩十艺节”标志即可获奖.
个大小相同的小球,分别印有“多彩十艺节”和“美丽泉城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球,若抽到两个球都印有“多彩十艺节”标志即可获奖.
(I)活动开始后,一位参加者问:盒中有几个“多彩十艺节”球?主持人笑说:我只知道从盒中同时抽两球不都是“美丽泉城行”标志的概率是 ,求抽奖者获奖的概率;
,求抽奖者获奖的概率;
(Ⅱ)上面条件下,现有甲、乙、丙、丁四人依次抽奖,抽后放回,另一个人再抽,用 表示获奖的人数,求
表示获奖的人数,求 的分布列及
的分布列及 .
.
已知函数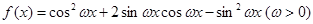 ,且周期为
,且周期为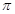 .
.
(1)求 的值;
的值;
(2)当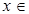 [
[ ]时,求
]时,求 的最大值及取得最大值时
的最大值及取得最大值时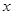 的值.
的值.
(本小题满分14分)设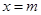 和
和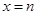 是函数
是函数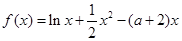 的两个极值点,其中
的两个极值点,其中 ,
, .
.
(1)若曲线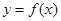 在点
在点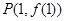 处的切线垂直于
处的切线垂直于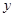 轴,求实数
轴,求实数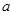 的值;
的值;
(2)求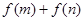 的取值范围;
的取值范围;
(3)若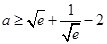 ,求
,求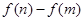 的最大值(
的最大值(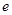 是自然对数的底数).
是自然对数的底数).
(本小题满分13分)在平面直角坐标系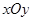 中,椭圆
中,椭圆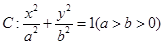 过点
过点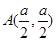 和点
和点 .
.
(1)求椭圆 的方程;
的方程;
(2)已知点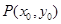 在椭圆
在椭圆 上,
上,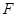 为椭圆的左焦点,直线
为椭圆的左焦点,直线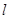 的方程为
的方程为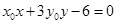 .
.
(i)求证:直线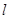 与椭圆
与椭圆 有唯一的公共点;
有唯一的公共点;
(ii)若点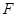 关于直线
关于直线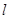 的对称点为
的对称点为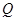 ,探索:当点
,探索:当点 在椭圆
在椭圆 上运动时,直线
上运动时,直线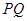 是否过定点?若过定点,求出此定点的坐标;若不过定点,请说明理由.
是否过定点?若过定点,求出此定点的坐标;若不过定点,请说明理由.
(本小题满分12分)已知在四棱锥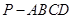 中,底面
中,底面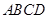 是矩形,且
是矩形,且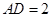 ,
,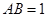 ,
,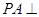 平面
平面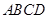 ,
,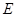 、
、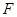 分别是线段
分别是线段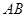 、
、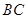 的中点.
的中点.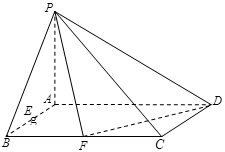
(1)证明: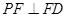 ;
;
(2)判断并说明 上是否存在点
上是否存在点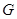 ,使得
,使得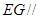 平面
平面 ?若存在,求出
?若存在,求出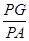 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分12分)某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.已知两组技工在单位时间内加工的合格零件平均数都为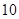 .
.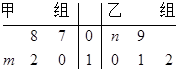
(1)分别求出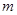 ,
,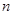 的值;
的值;
(2)分别求出甲、乙两组技工在单位时间内加工的合格零件的方差 和
和 ,并由此分析两组技工的加工水平;
,并由此分析两组技工的加工水平;
(3)质检部门从该车间甲、乙两组技工中各随机抽取一名技工,对其加工的零件进行检测,若两人
加工的合格零件个数之和大于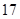 ,则称该车间“质量合格”,求该车间“质量合格”的概率.
,则称该车间“质量合格”,求该车间“质量合格”的概率.
(注:方差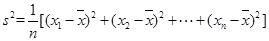 ,其中
,其中 为数据
为数据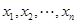 的平均数).
的平均数).