如图，抛物线y1＝－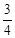
x2＋3与x轴交于A、B两点，与直线y2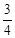＝－x＋b相交于B、C两点．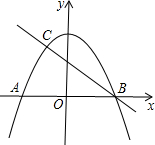
（1）求直线BC的解析式和点C的坐标；
（2）若对于相同的x，两个函数的函数值满足y1≥y2，则自变量x的取值范围是 ．
已知二次函数
（a＞0）的图象与x轴交于A（x1，0）、B（x2，0）（x1＜x2）两点，与y轴交于点C，x1，x2是方程
的两根．
（1）若抛物线的顶点为D，求S△ABC：S△ACD的值；
（2）若∠ADC=90°，求二次函数的解析式．
如图，在等边△ABC中，AB=3，D、E分别是AB、AC上的点，且DE∥BC，将△ADE沿DE翻折，与梯形BCED重叠的部分记作图形L．
（1）求△ABC的面积；
（2）设AD=x，图形L的面积为y，求y关于x的函数解析式；
（3）已知图形L的顶点均在⊙O上，当图形L的面积最大时，求⊙O的面积．
如图，AB是半圆O的直径，点P在BA的延长线上，PD切⊙O于点C，BD⊥PD，垂足为D，连接BC．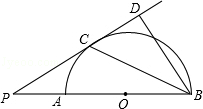
（1）求证：BC平分∠PDB；
（2）求证：BC2=AB•BD；
（3）若PA=6，PC=6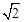
，求BD的长．
某地区为了进一步缓解交通拥堵问题，决定修建一条长为6千米的公路．如果平均每天的修建费y（万元）与修建天数x（天）之间在30≤x≤120，具有一次函数的关系，如下表所示．
| x |
50 |
60 |
90 |
120 |
| y |
40 |
38 |
32 |
26 |
（1）求y关于x的函数解析式；
（2）后来在修建的过程中计划发生改变，政府决定多修2千米，因此在没有增减建设力量的情况下，修完这条路比计划晚了15天，求原计划每天的修建费．
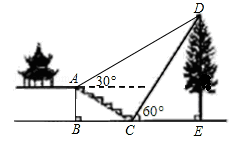
如图，某校综合实践活动小组的同学欲测量公园内一棵树DE的高度，他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得树顶端D的仰角为60°．已知A点的高度AB为3米，台阶AC的坡度为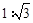
（即AB：BC=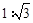），且B、C、E三点在同一条直线上．请根据以上条件求出树DE的高度（侧倾器的高度忽略不计）．