在长方体 中,
中,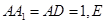 为线段
为线段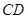 中点.
中点.
(1)求直线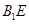 与直线
与直线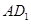 所成的角的余弦值;
所成的角的余弦值;
(2)若 ,求二面角
,求二面角 的大小;
的大小;
(3)在棱 上是否存在一点
上是否存在一点 ,使得
,使得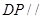 平面
平面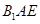 ?若存在,求
?若存在,求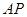 的长;若不存在,说明理由.
的长;若不存在,说明理由.
已知定点A(-2,0),动点B是圆 (F为圆心)上一点,线段AB的垂直平分线交BF于P.
(F为圆心)上一点,线段AB的垂直平分线交BF于P.
(1)求动点P的轨迹方程;
(2)是否存在过点E(0,-4)的直线l交P点的轨迹于点R,T,且满足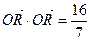 (O为原点),若存在,求直线l的方程,若不存在,请说明理由.
(O为原点),若存在,求直线l的方程,若不存在,请说明理由.
已知 ,动点
,动点 满足
满足 .
.
(Ⅰ)求动点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)过点 作直线
作直线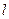 与曲线
与曲线 交于
交于 两点,若
两点,若 ,求直线
,求直线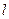 的方程;
的方程;
(Ⅲ)设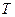 为曲线
为曲线 在第一象限内的一点,曲线
在第一象限内的一点,曲线 在
在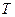 处的切线与
处的切线与
 轴分别交于点
轴分别交于点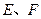 ,求
,求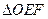 面积的最小值.
面积的最小值.
已知抛物线y=x2上的两点A、B满足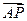 =l
=l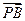 ,l>0,其中点P坐标为(0,1),
,l>0,其中点P坐标为(0,1), =
= +
+ ,O为坐标原点.
,O为坐标原点.
(I)求四边形OAMB的面积的最小值;
(II)求点M的轨迹方程.
设A,B分别是直线 和
和 上的两个动点,并且
上的两个动点,并且 ,动点P满足
,动点P满足 .记动点P的轨迹为C.
.记动点P的轨迹为C.
(I)求轨迹C的方程;
(II)若点D的坐标为(0,16),M、N是曲线C上的两个动点,且 ,求实数
,求实数 的取值范围.
的取值范围.
已知A.B是椭圆 上两点,O是坐标原点,定点
上两点,O是坐标原点,定点 ,向量
,向量 .
. 在向量
在向量 方向上的投影分别是m.n ,且
方向上的投影分别是m.n ,且 7mn ,动点P满足
7mn ,动点P满足
(Ⅰ)求点P的轨迹C的方程;
(Ⅱ)设过点E的直线l与C交于两个不同的点M.N,求 的取值范围。
的取值范围。