已知圆 ,若焦点在
,若焦点在 轴上的椭圆
轴上的椭圆 过点
过点 ,且其长轴长等于圆
,且其长轴长等于圆 的直径.
的直径.
(1)求椭圆的方程;
(2)过点 作两条互相垂直的直线
作两条互相垂直的直线 与
与 ,
, 与圆
与圆 交于
交于 、
、 两点,
两点, 交椭圆于另一点
交椭圆于另一点 ,设直线
,设直线 的斜率为
的斜率为 ,求弦
,求弦 长;
长;
(3)求 面积的最大值.
面积的最大值.
已知函数 .
.
(1)当 时,求曲线
时,求曲线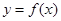 在点
在点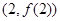 处的切线方程;
处的切线方程;
(2)当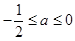 时,讨论
时,讨论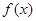 的单调性.
的单调性.
设函数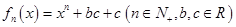 .
.
(1)设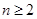 ,
,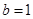 ,
,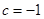 ,证明:
,证明: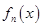 在区间
在区间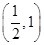 内存在唯一的零点;
内存在唯一的零点;
(2)设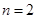 ,若对任意
,若对任意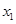 、
、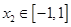 ,有
,有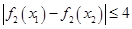 ,求
,求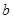 的取值范围.
的取值范围.
已知函数 ,其中
,其中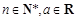 ,
,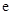 是自然对数的底数.
是自然对数的底数.
(1)求函数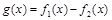 的零点;
的零点;
(2)若对任意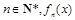 均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;
均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;
(3)已知 ,且函数
,且函数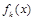 在R上是单调函数,探究函数
在R上是单调函数,探究函数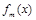 的单调性.
的单调性.
已知关于x的函数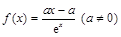
(1)当 时,求函数
时,求函数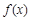 的极值;
的极值;
(2)若函数 没有零点,求实数a取值范围.
没有零点,求实数a取值范围.
对于函数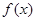 ,若在定义域存在实数
,若在定义域存在实数 ,满足
,满足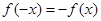 ,则称
,则称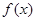 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数 ,试判断
,试判断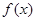 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)设 是定义在
是定义在 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数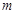 的取值范围.
的取值范围.