已知椭圆C的中心在原点,焦点在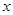 轴上,焦距为2,离心率为
轴上,焦距为2,离心率为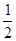
(1)求椭圆C的方程;
(2)设直线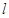 经过点
经过点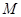 (0,1),且与椭圆C交于
(0,1),且与椭圆C交于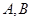 两点,若
两点,若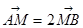 ,求直线
,求直线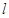 的方程.
的方程.
如图所示,若△ABC为等腰三角形,△ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上一点,且满足AB2=DB·CE.
(1)求证:△ADB∽△EAC;
(2)若∠BAC=40°,求∠DAE的度数.
如图,若BE∥CF∥DG,AB∶BC∶CD=1∶2∶3,CF=12 cm,求BE,DG的长.
如图所示,AB∥CD,OD2=OB·OE.
求证:AD∥CE.
(拓展深化)如图所示,AB是⊙O的直径,弦CD⊥AB于点P,CD=10 cm,AP∶PB=1∶5,求⊙O的半径.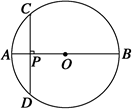
如图,已知在⊙O中,P是弦AB的中点,过点P作半径OA的垂线,垂足是点E.分别交⊙O于C、D两点. 
求证:PC·PD=AE·AO.