在平面直角坐标系xOy中,一块含60°角的三角板作如图摆放,斜边AB在x轴上,直角顶点C在y轴正半轴上,已知点A(-1,0).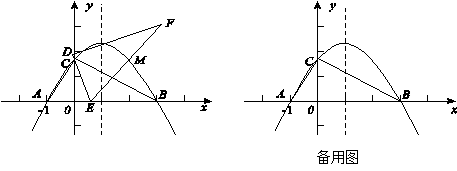
(1)请直接写出点B,C的坐标:B( , ),C( , );
(2)求经过A,B,C三点的抛物线解析式;
(3)现有与上述三角板完全一样的三角板DEF(其中∠EDF=90°,∠DEF=60°),把顶点E放在线段AB上(点E是不与A,B两点重合的动点),并使ED所在直线经过点C.此时,EF所在直线与(2)中的抛物线交于第一象限的点M.当AE=2时,抛物线的对称轴上是否存在点P使△PEM是等腰三角形,若存在,请求出点P的坐标;若不存在,请说明理由.
两块完全相同的三角形纸板ABC和DEF,按如图所示的方式叠放,阴影部分为重叠部分,点O为边
AC和DF的交点.不重叠的两部分△AOF与△DOC是否全等?为什么?
为了加强食品安全管理,有关部门对某大型超市的甲乙两种品牌食用油共抽取20瓶进行检测,检测结果分成“优秀”,“合格”,“不合格”三个等级,数据处理后制成以下折线统计图和扇形统计图
⑴甲乙两种品牌食用油各被抽取了多少瓶用于检测?
⑵在该超市购买一瓶甲品牌食用油,请估计能买到“优秀”等级的概率是多少?
如图,已知△ABC的两边长为m、n,夹角为α,求作△EFG,使得∠E=∠α;有两条边长分别为m、n,且与△ABC不全等.(要求:作出所有满足条件的△EFG,尺规作图,不写画法,保留作图痕迹.在图中标注m、n、 、E、F、G)
、E、F、G)
先化简,再求值: ,其中
,其中
如图,从顶点A出发,沿着边长为1的正方形的四个顶点依次跳舞,舞步长为1.第一次顺时针移动1步,第二次逆时针移动2步,第三次顺时针移动3步,……以此类推.
(1)移动4次后到达何处?(直接给出答案)
(2)移动2012次后到达何处?