如图，已知AB∥CD，分别探究下面四个图形中∠APC和∠PAB、∠PCD的关系，并从所得的四个关系中任选一个加以说明，证明所探究的结论的正确性.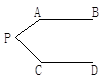
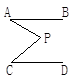
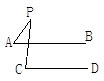
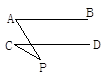
结论（1）____________________________；（2）____________________________；
（3）____________________________；（4）____________________________；
选择结论________，说明理由是什么.
如图，直线AD与AB、CD相交于A、D两点，EC、BF与AB、CD相交于E、C、B、F，如果∠1＝∠2，∠B＝∠C.说明∠A＝∠D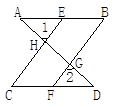
如图，已知DE∥BC，CD是∠ACB的平分线，∠B＝70°，∠ACB＝50°，求∠EDC和∠BDC的度数.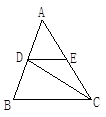
如图，已知∠B＝∠C，AE∥BC，说明AE平分∠CAD.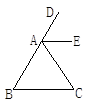
我们知道任何一个命题都由条件和结论两部分组成,如果我们把一个命题的条件变结论，结论变条件，那么所得的是不是一个命题?试举例说明.
是⊙
的直径，弦
，垂足为点
，点
是
上一点，且
．试判断
的形状，并说明你的理由．