例：说明代数式
的几何意义，并求它的最小值．
解：
，如图，建立平面直角坐标系，点P（x，0）是x轴上一点，则
可以看成点P与点A（0，1）的距离，
可以看成点P与点B（3，2）的距离，所以原代数式的值可以看成线段PA与PB长度之和，它的最小值就是PA＋PB的最小值．
设点A关于x轴的对称点为A′，则PA＝PA′，因此，求PA＋PB的最小值，
只需求PA′＋PB的最小值，而点A′、B间的直线段距离最短，
所以PA′＋PB的最小值为线段A′B的长度．为此，构造直角
三角形A′CB，因为A′C＝3，CB＝3，所以A′B＝
，
即原式的最小值为。
根据以上阅读材料，解答下列问题：
（1）代数式
的值可以看成平面直角坐标系中点P（x，0）与点A（1，1）、点B 的距离之和．（填写点B的坐标）
（2）求代数式
的最小值
如果a2﹣2（k﹣1）ab+9b2是一个完全平方式，那么k= _________ ．
如图1，是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后按图2的形状拼成一个正方形．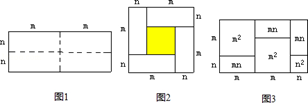
（1）图2中阴影部分的面积为 （m﹣n）2 ；
（2）观察图2，请你写出三个代数式（m+n）2、（m﹣n）2、mn之间的等量关系式： （m﹣n）2+4mn=（m+n）2 ；
（3）根据（2）中的结论，若x+y=﹣6，xy=2.75，则x﹣y= ±5 ．
（4）有许多代数恒等式可以用图形的面积来表示．如图3，它表示了（2m+n）（m+n）=2m2+3mn+n2．试画出一个几何图形，使它的面积能表示（m+n）（m+3n）=m2+4mn+3n2．
观察如图图形由左到右的变化，计算阴影部分的面积，并用面积的不同表达形式写出相应的代数恒等式．
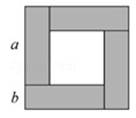
图①是一个长为2a，宽为2b的长方形，沿图中虚线用剪刀均分成四个小长方形，然后按图②的形状拼成一个正方形．
（1）图②中阴影部分的正方形的边长是 _________ ；
（2）请用两种不同的方法求图2中阴影部分的面积：
方法1： _________ ；
方法2： _________ ；
（3）观察图②，请你写出（a+b）2、（a﹣b）2、ab之间的等量关系是 _________ ；
（4）根据（3）中的等量关系解决如下问题：若m﹣n=﹣5，mn=3，则（m+n）2的值为多少？
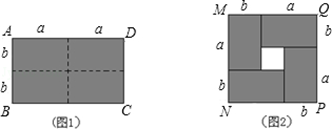
通常，我们把长方形和正方形统称为矩形．如图1，是一个长为2a，宽为2b的矩形ABCD，若把此矩形沿图中的虚线用剪刀均分为4块小长方形，然后按照图2的形状拼成一个正方形MNPQ．
（1）分别从整体和局部的角度出发，计算图2中阴影部分的面积，可以得到等式 _________ ．
（2）仔细观察长方形ABCD与正方形MNPQ，可以发现它们的 _________ 相同， _________ 不同．（选填“周长”或“面积”）
（3）根据上述发现，猜想结论：用总长为36米的篱笆围成一个矩形养鸡场，可以有许多不同的围法．在你围的所有矩形中，面积最大的矩形的面积是 _________ 米2．