已知点 (
( ,
, 是常数),且动点
是常数),且动点 到
到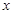 轴的距离比到点
轴的距离比到点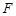 的距离小
的距离小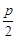 .
.
(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)(i)已知点 ,若曲线
,若曲线 上存在不同两点
上存在不同两点 、
、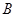 满足
满足 ,求实数
,求实数 的取值范围;
的取值范围;
(ii)当 时,抛物线
时,抛物线 上是否存在异于
上是否存在异于 、
、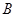 的点
的点 ,使得经过
,使得经过 、
、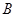 、
、 三点的圆和抛物线
三点的圆和抛物线 在点
在点 处有相同的切线,若存在,求出点
处有相同的切线,若存在,求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
(本小题满分14分)在平面直角坐标系中, 为坐标原点,已知向量
为坐标原点,已知向量 ,又点
,又点 .
.
(1)若 ,且
,且 ,求向量
,求向量 ;
;
(2)若向量 与向量
与向量 共线,当
共线,当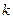
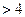 时,且
时,且 取最大值为4时,求
取最大值为4时,求 .
.
(本小题满分12分)已知 ,
, ,且
,且 //
//  .设函数
.设函数 .
.
(1)求函数 的解析式;
的解析式;
(2)若在锐角 中,
中, ,边
,边 ,求
,求 周长的最大值.
周长的最大值.
(本小题满分12分)已知函数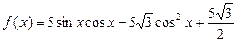 .
.
(1)确定函数f(x)的单调增区间;
(2)将函数y=f(x)的图象向左平移 个单位长度,所得图象关于y轴对称,求φ的值。
个单位长度,所得图象关于y轴对称,求φ的值。
. 根据如图所示的程序框图,将输出的x、y值依次分别
记为 y1,y2,…,yn,…,y2007
y1,y2,…,yn,…,y2007
(1)求数列 的通项公式
的通项公式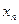 ;
;
(2)写出y1,y2,y3,y4,由此猜想出数列{yn}的一个
通项公式yn,并证明你的结论;
(3)求
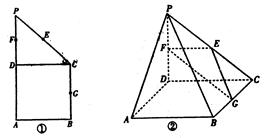
如图①在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E,F,G分别是线段PC、PD,BC的中点,现将ΔPDC折起,使平面PDC⊥平面ABCD(如图②)
(1)求证AP∥平面EFG;
(2)求直线AP与平面EFG之间的距离;
(3)在线段PB上确定一点Q,使PC⊥平面ADQ,试给出证明.