下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.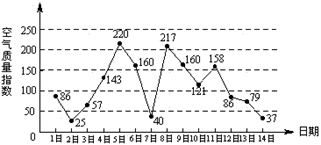
(Ⅰ)求此人到达当日空气重度污染的概率;
(Ⅱ)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望.
(本小题满分12分)
甲、乙两名射击运动员,甲射击一次命中10环的概率为 ,乙射击一次命中10环的概率为s,若他们各自独立地射击两次,设乙命中10环的次数为ξ,且ξ的数学期望Eξ=
,乙射击一次命中10环的概率为s,若他们各自独立地射击两次,设乙命中10环的次数为ξ,且ξ的数学期望Eξ= ,
, 表示甲与乙命中10环的次数的差的绝对值.
表示甲与乙命中10环的次数的差的绝对值.
(1)求s的值及 的分布列, (2)求
的分布列, (2)求 的数学期望.
的数学期望.
(本小题满分12分)
如图,函数f1(x)=A sin(wx+j)(A>0,w>0,|j|<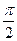 )的一段图象,过点(0,1).(1)求函数f1(x)的解析式;(2)将函数y=f1(x)的图象按向量
)的一段图象,过点(0,1).(1)求函数f1(x)的解析式;(2)将函数y=f1(x)的图象按向量 =
=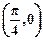 平移,得到函数y=f2(x),求y=f1(x)+f2(x)的最大值,并求此时自变量x的集合.
平移,得到函数y=f2(x),求y=f1(x)+f2(x)的最大值,并求此时自变量x的集合.
(本小题满分13分)已知椭圆的中心在原点O,短轴长为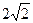 ,其焦点F(c,0)(c>0)对应的准线l与x轴交于A点,|OF|=2|FA|,过A的直线与椭圆交于P、Q两点.
,其焦点F(c,0)(c>0)对应的准线l与x轴交于A点,|OF|=2|FA|,过A的直线与椭圆交于P、Q两点.
(1)求椭圆的方程;(2)若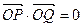 ,求直线PQ的方程;(3)设
,求直线PQ的方程;(3)设 ,过点P且平行于准线l的直线与椭圆相交于另一点M. 求证F、M、Q三点共线.
,过点P且平行于准线l的直线与椭圆相交于另一点M. 求证F、M、Q三点共线.
(本小题满分12分)
已知函数 =
= ,在
,在 处取得极值2。
处取得极值2。
(1)求函数 的解析式;
的解析式;
(2) 满足什么条件时,区间
满足什么条件时,区间 为函数
为函数 的单调增区间?
的单调增区间?
(3)若 为
为 =
= 图象上的任意一点,直线
图象上的任意一点,直线 与
与 =
= 的图象切于
的图象切于 点,求直线
点,求直线 的斜率的取值范围。
的斜率的取值范围。
(本小题满分12分)
在一次篮球练习课中,规定每人最多投篮5次,若投中2次就称为“通过”,若投中3次就称为“优秀”并停止投篮.已知甲每次投篮投中的概率是 .
.
(I)求甲恰好投篮3次就通过的概率;
(II)设甲投篮投中的次数为 ,求随机变量
,求随机变量 的分布列及数学期望E
的分布列及数学期望E .
.