在△ABC中,角A、B、C所对的边分别为a、b、c,且b2+c2=a2+bc.
(1)求角A的大小;(2)若sinB·sinC=sin2A,试判断△ABC的形状.
右图为一组合体,其底面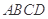 为正方形,
为正方形, 平面
平面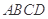 ,
,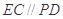 ,且
,且
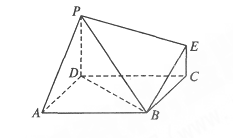
(Ⅰ)求证: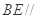 平面
平面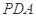 ;
;
(Ⅱ)求四棱锥 的体积;
的体积;
(Ⅲ)求该组合体的表面积.
已知向量 ,向量
,向量 ,函数
,函数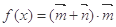 .
.
(1)求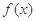 的最小正周期
的最小正周期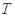 ;
;
(2)已知 分别为
分别为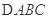 内角
内角 的对边,
的对边, 为锐角,
为锐角,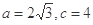 ,且
,且 恰是
恰是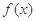 在
在 上的最大值,求
上的最大值,求 和
和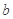 的值.
的值.
已知等差数列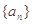 中,公差
中,公差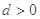 ,其前
,其前 项和为
项和为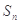 ,且满足:
,且满足: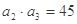 ,
,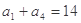 .
.
(Ⅰ)求数列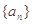 的通项公式;
的通项公式;
(Ⅱ)令 ,
, (
( ),求
),求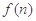 的最大值.
的最大值.
已知 .
.
(1)曲线y=f(x)在x=0处的切线恰与直线 垂直,求
垂直,求 的值;
的值;
(2)若x∈[a,2a]求f(x)的最大值;
(3)若f(x1)=f(x2)=0(x1<x2),求证: .
.
如图,已知椭圆 的长轴为AB,过点B的直线
的长轴为AB,过点B的直线 与
与
轴垂直,椭圆的离心率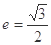 ,F为椭圆的左焦点,且
,F为椭圆的左焦点,且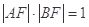

(1)求此椭圆的标准方程;
(2)设P是此椭圆上异于A,B的任意一点, 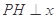 轴,H为垂足,延长HP到点Q,使得HP=PQ,连接AQ并延长交直线
轴,H为垂足,延长HP到点Q,使得HP=PQ,连接AQ并延长交直线 于点
于点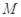 ,
,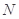 为
为 的中点,判定直线
的中点,判定直线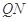 与以
与以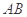 为直径的圆O位置关系。
为直径的圆O位置关系。