已知 .
.
(1)曲线y=f(x)在x=0处的切线恰与直线 垂直,求
垂直,求 的值;
的值;
(2)若x∈[a,2a]求f(x)的最大值;
(3)若f(x1)=f(x2)=0(x1<x2),求证: .
.
已知某圆的极坐标方程是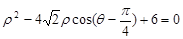 ,求:
,求:
(1)求圆的普通方程和一个参数方程;
(2)圆上所有点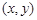 中
中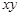 的最大值和最小值.
的最大值和最小值.
如图所示,△ABC内接于⊙O,AB=AC,直线XY切⊙O于点C,BD∥XY,AC、BD相交于E.
(1)求证:△ABE≌△ACD;
(2)若AB=6 cm,BC=4 cm,求AE的长.
为了解某班学生关注NBA是否与性别有关,对本班48人进行了问卷调查得到如下的列联表:
| 关注NBA |
不关注NBA |
合计 |
|
| 男生 |
6 |
||
| 女生 |
10 |
||
| 合计 |
48 |
已知在全班48人中随机抽取1人,抽到关注NBA的学生的概率为2/3
⑴请将上面列连表补充完整,并判断是否有 的把握认为关注NBA与性别有关?
的把握认为关注NBA与性别有关?
⑵现从女生中抽取2人进一步调查,设其中关注NBA的女生人数为X,求X的分布列与数学期望.
附: ,其中
,其中 
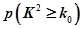 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
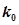 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
函数
(1)a=0时,求f(x)最小值;
(2)若f(x)在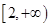 是单调减函数,求a的取值范围.
是单调减函数,求a的取值范围.
已知甲盒内有大小相同的1个红球和3个黑球, 乙盒内有大小相同的2个红球和4个黑球,现从甲、乙两个盒内各任取2个球.
(1)求取出的4个球均为黑球的概率;
(2)求取出的4个球中恰有1个红球的概率;
(3)设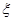 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求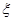 的分布列和数学期望
的分布列和数学期望