已知甲盒内有大小相同的1个红球和3个黑球, 乙盒内有大小相同的2个红球和4个黑球,现从甲、乙两个盒内各任取2个球.
(1)求取出的4个球均为黑球的概率;
(2)求取出的4个球中恰有1个红球的概率;
(3)设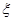 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求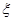 的分布列和数学期望
的分布列和数学期望
已知等比数列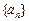 的公比大于1,
的公比大于1,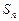 是数列
是数列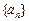 的前n项和,
的前n项和,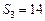 ,且
,且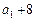 ,
,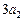 ,
,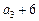 依次成等差数列,数列
依次成等差数列,数列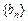 满足:
满足: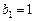 ,
,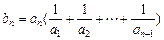
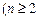 )
)
(1) 求数列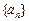 、
、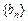 的通项公式;
的通项公式;
(2)求数列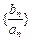 的前n项和为
的前n项和为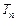
已知函数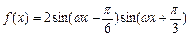
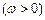 的最小正周期为
的最小正周期为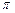
(1) 若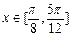 ,求函数
,求函数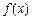 的最小值;
的最小值;
(2) 在△ABC中,若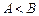 ,且
,且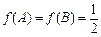 ,求
,求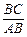 的值
的值
已知函数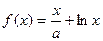 ,其中
,其中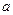 为常数,
为常数,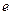 为自然对数的底数.
为自然对数的底数.
(Ⅰ)当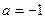 时,求
时,求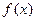 的单调区间;
的单调区间;
(Ⅱ)若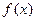 在区间
在区间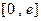 上的最大值为2,求
上的最大值为2,求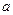 的值.
的值.
.已知椭圆C: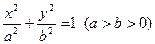 的离心率为
的离心率为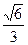 ,椭圆C上任意一点到椭圆两个焦点的距离之和为6.
,椭圆C上任意一点到椭圆两个焦点的距离之和为6.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线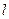 :
: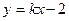 与椭圆C交于
与椭圆C交于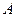 ,
,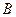 两点,点
两点,点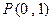 ,且
,且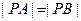 ,求直线
,求直线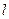 的方程.
的方程.
某班主任对班级22名学生进行了作业量多少的调查,数据如下:在喜欢玩电脑游戏的12中,有9人认为作业多,3人认为作业不多;在不喜欢玩电脑游戏的10人中,有4人认为作业多,6人认为作业不多.
(Ⅰ)根据以上数据建立一个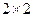 列联表;
列联表;
(Ⅱ)试问喜欢电脑游戏与认为作业多少是否有关系?
(可能用到的公式: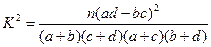 ,可能用到数据:
,可能用到数据: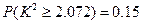 ,
,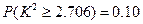 ,
,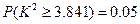 ,
,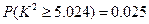 .)
.)