等差数列 中,
中, ,公差
,公差 ,且它的第2项,第5项,第14项分别是等比数列
,且它的第2项,第5项,第14项分别是等比数列 的第2项,第3项,第4项.
的第2项,第3项,第4项.
(Ⅰ)求数列 与
与 的通项公式;
的通项公式;
(Ⅱ)设数列 对任意自然数均有
对任意自然数均有 成立,求
成立,求 的值.
的值.
设 ,
,
(1)当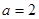 时,求曲线
时,求曲线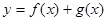 在
在 处的切线方程
处的切线方程
(2)如果对任意的 ,恒有
,恒有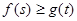 成立,求实数
成立,求实数 的取值范围
的取值范围
(1) ,
, 则
则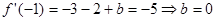
(2)由(1)知 ,则
,则
①当 时,
时, ,令
,令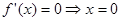 或
或
 ,
,
 在
在 上的值域为
上的值域为
② 当 时, a.若
时, a.若 ,则
,则
b.若 ,则
,则 在
在 上是单调减的
上是单调减的
 在
在 上的值域为
上的值域为
c.若 则
则 在
在 上是单调增的
上是单调增的
 在
在 上的值域为
上的值域为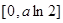
综上所述,当 时,
时, 在
在 的值域为
的值域为
当 时,
时, 在
在 的值域为
的值域为
当 时,若
时,若

 时,
时, 在
在 的值域为
的值域为
若

 时,
时, 在
在 的值域为
的值域为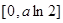
即当 时,
时, 在
在 的值域为
的值域为
当 时,
时, 在
在 的值域为
的值域为
当 时,
时, 在
在 的值域为
的值域为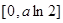
已知函数 的图像过坐标原点
的图像过坐标原点 ,且在点
,且在点 处的切线的斜率是
处的切线的斜率是 .
.
(1)求实数 ,
, 的值
的值
(2)求 在区间
在区间 上的值域
上的值域
已知函数
(1)求 的极大值和极小值,并画出函数
的极大值和极小值,并画出函数 的草图
的草图
(2)根据函数图象讨论方程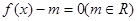 的根的个数问题:
的根的个数问题:
①有且仅有两个不同的实根,求 的取值范围
的取值范围
②有且仅有一个实根,求 的取值范围
的取值范围
③无实根,求 的取值范围
的取值范围
已知数列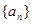 满足a1=1,an+1>an,且(an+1-an)2-2(an+1+an)+1=0
满足a1=1,an+1>an,且(an+1-an)2-2(an+1+an)+1=0
(1)求a2、a3
(2)猜想 的表达式,并用数学归纳法证明你的结论
的表达式,并用数学归纳法证明你的结论