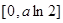(1) ,
, 则
则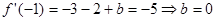
(2)由(1)知 ,则
,则
①当 时,
时, ,令
,令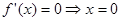 或
或
 ,
,
 在
在 上的值域为
上的值域为
② 当 时, a.若
时, a.若 ,则
,则
b.若 ,则
,则 在
在 上是单调减的
上是单调减的
 在
在 上的值域为
上的值域为
c.若 则
则 在
在 上是单调增的
上是单调增的
 在
在 上的值域为
上的值域为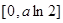
综上所述,当 时,
时, 在
在 的值域为
的值域为
当 时,
时, 在
在 的值域为
的值域为
当 时,若
时,若

 时,
时, 在
在 的值域为
的值域为
若

 时,
时, 在
在 的值域为
的值域为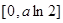
即 当 时,
时, 在
在 的值域为
的值域为
当 时,
时, 在
在 的值域为
的值域为
当 时,
时, 在
在 的值域为
的值域为