如图,BC是⊙O的弦,OD⊥BC于E,交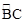 于D,点A是优弧
于D,点A是优弧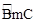 上的动点(不与B、C重合),BC=
上的动点(不与B、C重合),BC=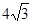 ,ED=2.
,ED=2.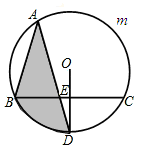
(1)求⊙O的半径;
(2)求cos∠A的值及图中阴影部分面积的最大值.
如图,反比例函数y= (k<0)的图象与矩形ABCD的边相交于E、F两点,且BE=2AE,E(﹣1,2).
(k<0)的图象与矩形ABCD的边相交于E、F两点,且BE=2AE,E(﹣1,2).
(1)求反比例函数的解析式;
(2)连接EF,求△BEF的面积.
如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.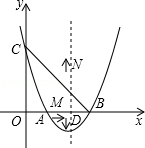
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形?若存在.请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.
如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.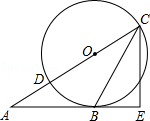
(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径.
2015年5月,某县突降暴雨,造成山体滑坡,挢梁垮塌,房屋大面积受损,该省民政厅急需将一批帐篷送往灾区.现有甲、乙两种货车,己知甲种货车比乙种货车每辆车多装20件帐篷,且甲种货车装运1000件帐篷所用车辆与乙种货车装运800件帐蓬所用车辆相等.
(1)求甲、乙两种货车每辆车可装多少件帐蓬?
(2)如果这批帐篷有1490件,用甲、乙两种汽车共16辆来装运,甲种车辆刚好装满,乙种车辆最后一辆只装了50件,其它装满,求甲、乙两种汽车各有多少辆?
如图,一艘轮船航行到B处时,测得小岛A在船的北偏东60°的方向,轮船从B处继续向正东方向航行200海里到达C处时,测得小岛A在船的北偏东30°的方向.己知在小岛周围170海里内有暗礁,若轮船不改变航向继续向前行驶,试问轮船有无触礁的危险?( ≈1.732)
≈1.732)