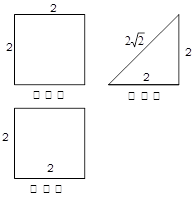某连锁分店销售某种商品,每件商品的成本为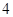 元,并且每件商品需向总店交
元,并且每件商品需向总店交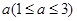 元的管理费,预计当每件商品的售价为
元的管理费,预计当每件商品的售价为 元时,一年的销售量为
元时,一年的销售量为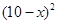 万件.
万件.
(1)求该连锁分店一年的利润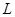 (万元)与每件商品的售价
(万元)与每件商品的售价 的函数关系式
的函数关系式 ;
;
(2)当每件商品的售价为多少元时,该连锁分店一年的利润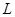 最大,并求出
最大,并求出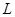 的最大值.
的最大值.
直四棱柱 中,底面
中,底面 是等腰梯形,
是等腰梯形,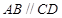 ,
,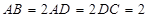 ,
,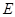 为
为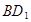 的中点,
的中点, 为
为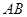 中点.
中点.
(1) 求证: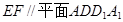 ;
;
(2) 若 ,求
,求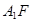 与平面
与平面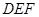 所成角的正弦值.
所成角的正弦值.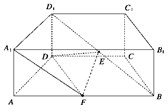
已知函数
(I)求函数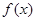 的最小值和最小正周期;
的最小值和最小正周期;
(II)已知 内角
内角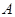 ,
,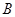 ,
, 的对边分别为
的对边分别为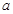 ,
,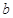 ,
, ,且
,且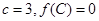 ,若向量
,若向量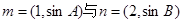 共线,求
共线,求 的值。
的值。
..(本小题满分14分)定义在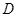 上的函数
上的函数 ,如果满足;对任意
,如果满足;对任意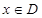 ,存在常数
,存在常数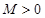 ,都有
,都有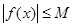 成立,则称
成立,则称 是
是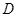 上的有界函数,其中
上的有界函数,其中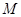 称为函数
称为函数 的上界.已知函数
的上界.已知函数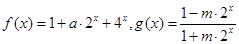 .
.
(Ⅰ)当 时,求函数
时,求函数 在
在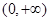 上的值域,并判断函数
上的值域,并判断函数 在
在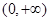 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(Ⅱ)若 是
是 上的有界函数,且
上的有界函数,且 的上界为3,求实数
的上界为3,求实数 的取值范围;
的取值范围;
(Ⅲ)若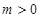 ,求函数
,求函数 在
在 上的上界
上的上界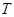 的取值范围.
的取值范围.
..(本小题满分14分)坐标法是解析几何中最基本的研究方法,坐标法是以坐标系为桥梁,把几何问题转化成代数问题,通过代数运算研究几何图形性质的方法.请利用坐标法解决以下问题:
(Ⅰ)在直角坐标平面内,已知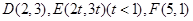 ,对任意
,对任意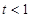 ,试判断
,试判断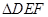 的形状;
的形状;
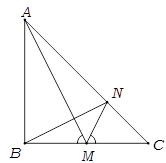
(Ⅱ)在平面内,已知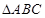 中,
中,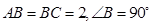 ,
,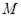 为
为 的中点,
的中点,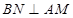 交
交 于
于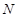 ,求证:
,求证: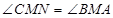 .
.
.(本小题满分13分)一个几何体的直观图及三视图如图所示,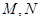 分别是
分别是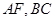 的中点.
的中点.
(Ⅰ)写出这个几何体的名称;
(Ⅱ)求证: ;
;
(Ⅲ)求多面体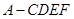 的体积.
的体积.