直四棱柱 中,底面
中,底面 是等腰梯形,
是等腰梯形,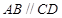 ,
,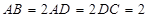 ,
,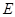 为
为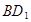 的中点,
的中点, 为
为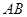 中点.
中点.
(1) 求证: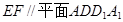 ;
;
(2) 若 ,求
,求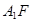 与平面
与平面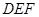 所成角的正弦值.
所成角的正弦值.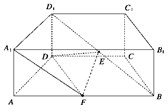
已知幂函数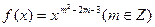 为偶函数且在区间(0,+∞)上是单调递减函数。(1)求函数f(x)的解析式;(2)讨论函数
为偶函数且在区间(0,+∞)上是单调递减函数。(1)求函数f(x)的解析式;(2)讨论函数 的奇偶性。(10分)
的奇偶性。(10分)
(本小题满分12分)
定义在D上的函数 ,如果满足:对任意
,如果满足:对任意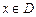 ,存在常数
,存在常数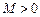 ,都有
,都有 成立,则称
成立,则称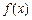 是D上的有界函数,其中M称为函数
是D上的有界函数,其中M称为函数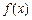 的上界.
的上界.
已知函数 ;
; .
.
(1)当a=1时,求函数 在
在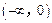 上的值域,并判断函数
上的值域,并判断函数 在
在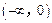 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数 在
在 上是以3为上界的有界函数,求实数a的取值范围;
上是以3为上界的有界函数,求实数a的取值范围;
(3)若 ,函数
,函数 在
在 上的上界是
上的上界是 ,求
,求 的取值范围.
的取值范围.
(本小题满分12分)
定义在R上的函数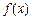 满足:对任意实数m,n,总有
满足:对任意实数m,n,总有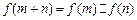 ,且当
,且当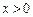 时,
时,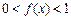 .
.
(1)试求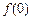 的值;
的值;
(2)判断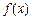 的单调性并证明你的结论;
的单调性并证明你的结论;
(3)若不等式 对
对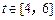 恒成立,求实数x的取值范围.
恒成立,求实数x的取值范围.
(本小题满分12分)
某公司是专门生产健身产品的企业,第一批产品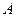 上市销售40天内全部售完,该公司对第一批产品
上市销售40天内全部售完,该公司对第一批产品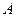 上市后的市场销售进行调研,结果如图(1)、(2)所示.其中(1)的抛物线表示的是市场的日销售量与上市时间的关系;(2)的折线表示的是每件产品
上市后的市场销售进行调研,结果如图(1)、(2)所示.其中(1)的抛物线表示的是市场的日销售量与上市时间的关系;(2)的折线表示的是每件产品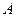 的销售利润与上市时间的关系.
的销售利润与上市时间的关系.
(1)写出市场的日销售量 与第一批产品A上市时间t的关系式;
与第一批产品A上市时间t的关系式;
(2)第一批产品A上市后的第几天,这家公司日销售利润最大,最大利润是多少?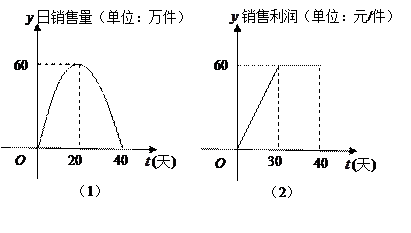
(本小题满分13分)
已知奇函数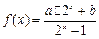 的反函数
的反函数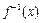 的图象过点
的图象过点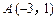 .
.
(1)求实数a,b的值;
(2)解关于x的不等式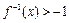 .
.