如图所示,一种医用输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下球状液体,其中球状液体的半径 毫米,滴管内液体忽略不计.
毫米,滴管内液体忽略不计.
(1)如果瓶内的药液恰好 分钟滴完,问每分钟应滴下多少滴?
分钟滴完,问每分钟应滴下多少滴?
(2)在条件(1)下,设输液开始后 (单位:分钟),瓶内液面与进气管的距离为
(单位:分钟),瓶内液面与进气管的距离为 (单位:厘米),已知当
(单位:厘米),已知当 时,
时, .试将
.试将 表示为
表示为 的函数.(注:
的函数.(注: )
)
设函数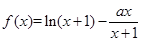 ,
,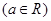 ;
; ,
, .
.
(1)求函数 的单调区间;
的单调区间;
(2)当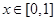 时,求函数
时,求函数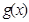 的最大值;
的最大值;
(3)求证: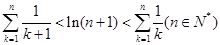
如图,已知椭圆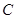 :
: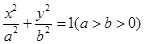 的离心率为
的离心率为 ,以椭圆
,以椭圆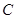 的左顶点
的左顶点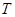 为圆心作圆
为圆心作圆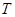 :
: ,设圆
,设圆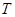 与椭圆
与椭圆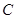 交于点
交于点 与点
与点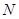 .
.
(1)求椭圆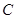 的方程;
的方程;
(2)求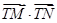 的最小值,并求此时圆
的最小值,并求此时圆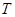 的方程;
的方程;
(3)设点 是椭圆
是椭圆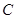 上异于
上异于 ,
,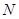 的任意一点,且直线
的任意一点,且直线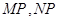 分别与
分别与 轴交于点
轴交于点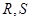 ,
, 为坐标原点,求证:
为坐标原点,求证: 为定值.
为定值.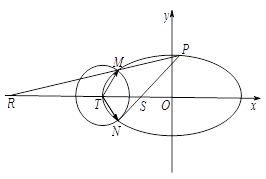
若数列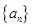 的前
的前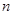 项和为
项和为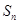 ,对任意正整数
,对任意正整数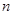 都有
都有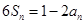 记
记 .
.
(1)求 ,
, 的值;
的值;
(2)求数列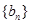 的通项公式;
的通项公式;
(3)令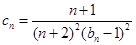 ,数列
,数列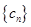 的前
的前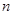 项和为
项和为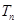 ,证明:对于任意的
,证明:对于任意的 ,都有
,都有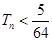 .
.
如图,在四棱锥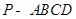 中,
中,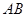 //
// ,
,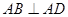 ,
, ,
,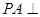 平面
平面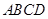 ,
,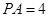 .
.
(1)求证: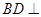 平面
平面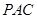 ;
;
(2)设点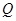 为线段
为线段 上一点,且直线
上一点,且直线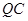 与平面
与平面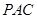 所成角的正弦值为
所成角的正弦值为 ,求
,求 的值.
的值.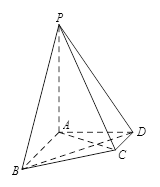
某市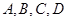 四所中学报名参加某高校今年自主招生的学生人数如下表所示:
四所中学报名参加某高校今年自主招生的学生人数如下表所示:
| 中学 |
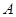 |
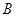 |
 |
 |
| 人数 |
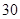 |
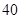 |
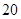 |
 |
为了了解参加考试的学生的学习状况,该高校采用分层抽样的方法从报名参加考试的四所中学的学生当中随机抽取50名参加问卷调查.
(1)问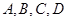 四所中学各抽取多少名学生?
四所中学各抽取多少名学生?
(2)在参加问卷调查的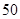 名学生中,从来自
名学生中,从来自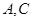 两所中学的学生当中随机抽取两名学生,用
两所中学的学生当中随机抽取两名学生,用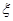 表示抽得
表示抽得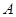 中学的学生人数,求
中学的学生人数,求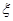 的分布列,数学期望和方差.
的分布列,数学期望和方差.