已知等比数列 的公比为
的公比为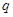 ,
, 是
是 的前
的前 项和.
项和.
(1)若 ,
,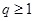 ,求
,求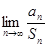 的值;
的值;
(2)若 ,
,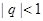 ,
, 有无最值?并说明理由;
有无最值?并说明理由;
(3)设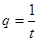 ,若首项
,若首项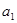 和
和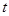 都是正整数,
都是正整数,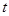 满足不等式:
满足不等式: ,且对于任意正整数
,且对于任意正整数 有
有 成立,问:这样的数列
成立,问:这样的数列 有几个?
有几个?
掷两枚骰子,求所得的点数之和为6的概率.
设f(x)=x3+3x2+px, g(x)=x3+qx2+r,且y=f(x)与y=g(x)的图象关于点(0,1)对称.(1)求p、q、r的值;(2)若函数g(x)在区间(0,m)上递减,求m的取值范围;(3)若函数g(x)在区间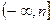 上的最大值为2,求n的取值范围.
上的最大值为2,求n的取值范围.
知函数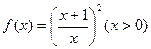 .
.
(1)求函数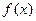 的反函数
的反函数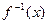 ;
;
(2)若 时,不等式
时,不等式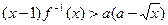 恒成立,试求实数
恒成立,试求实数 的范围.
的范围.
设f(x)=ax2+bx+c(a>b>c),f(1)=0,g(x)=ax+b.
(1)求证:函数y=f(x)与y=g(x)的图象有两个交点;
(2)设f(x)与g(x)的图象交点A、B在x轴上的射影为A1、B1,求|A1B1|的取值范围;
已知函数 在
在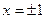 处取得极值.
处取得极值.
(1)讨论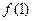 和
和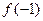 是函数
是函数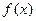 的极大值还是极小值;
的极大值还是极小值;
(2)过点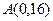 作曲线
作曲线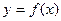 的切线,求此切线方程.
的切线,求此切线方程.