张大伯计划建一个面积为72平方米的矩形养鸡场，为了节约材料，鸡场一边靠着原有的一堵墙（墙长15米），另外的部分（包括中间的隔墙）用30米的竹篱笆围成，如图．
（1）请你通过计算帮助张大伯设计出围养鸡场的方案．
（2）在上述条件不变的情况下，能围出比72平方米更大的养鸡场吗？请说明理由．
如图，AB是⊙O的直径，C是
的中点，CE⊥AB于E，BD交CE于点F．
（1）求证：CF﹦BF；
（2）若CD﹦6，AC﹦8，则⊙O的半径为，CE的长是．
如图所示，⊙O的直径AB长为6，弦AC长为2，∠ACB的平分线交⊙O于点D，求四边形ADBC的面积．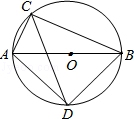
正方形ABCD的四个顶点都在⊙O上，E是⊙O上的一点．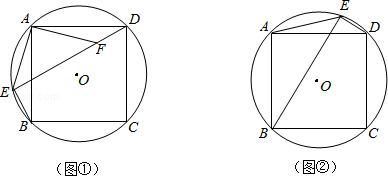
（1）如图①，若点E在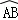
上，F是DE上的一点，DF=BE．求证：△ADF≌△ABE；
（2）在（1）的条件下，小明还发现线段DE、BE、AE之间满足等量关系：DE﹣BE=
AE．请你说明理由；
（3）如图②，若点E在
上．写出线段DE、BE、AE之间的等量关系．（不必证明）
如图，等边△ABC内接于⊙O，P是
上任一点（点P不与点A、B重合），连AP、BP，过点C作CM∥BP交PA的延长线于点M．
（1）填空：∠APC=度，∠BPC=度；
（2）求证：△ACM≌△BCP；
（3）若PA=1，PB=2，求梯形PBCM的面积．
如图，AB是⊙O的直径，
=
，∠COD=60°．
（1）△AOC是等边三角形吗？请说明理由；
（2）求证：OC∥BD．