如图所示，ABDO是处于竖直平面内的光滑轨道，AB是半径为R=15m的1/4圆周轨道，半径OA处于水平位置，BDO是直径为15m的半圆轨道，D为BDO轨道的中央。一个小球P从A点的正上方距水平半径OA高H处自由落下，沿竖直平面内的轨道通过D点时对轨道的压力等于其重力的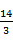
倍。取g=10m/s2。
（1）H的大小？
（2）试讨论此球能否到达BDO轨道的O点，并说明理由。
（3）小球沿轨道运动后再次落到轨道上的速度的大小是多少？
如图所示，质量为M的木框内静止在地面上，劲度系数为k的轻质弹簧一端固定于木框，一质量为m的小球放在该弹簧上，让小球在同一条
竖直线上作简谐运动，在此过程中木框始终没有离开地面。若使小球始终不脱离弹簧，则：
（1）小球的最大振幅A是多大？
（
2）在这个振幅下木框对地面的最大压力是多少？
（3）在这个振幅下弹簧的最大弹性势能是多大？
如图所示，两电阻不计的足够长光滑平行金属导轨与水平面夹角为
，导轨间距为l，所在平面的正方形区域abcd内存在有界匀强磁场，磁感应强度大小为B，方向垂直于斜面向上。如图所示，将甲、乙两阻值相同，质量均为m的相同金属杆放置在导轨上，甲金属杆处在磁场的上边界，甲、乙相距l。从静止释放两金属杆的同时，在金属杆上施加一个沿着导轨的外力，使甲金属杆在运动过程中始终沿导轨向下做匀加速直线运动，且加速度大小以
，乙金属杆刚进入磁场时做匀速运动。
（1）求每根金属杆的电阻R为多少?
（2）从刚释放金属杆时开始计时，写出从计时开始到甲金属杆离开磁场的过程中外力F随时间t的变化关系式，并说明F的方向。
（3）若从开始释放到两杆到乙金属杆离开磁场，乙金属杆共产生热量Q，试求此过程中外力F对甲做的功。
如图所示，ABC和DEF是在同一竖直平面内的两条光滑轨道，其中ABC的末端水平，DEF是半径为r=0．4 m的半圆形轨道，其直径DF沿竖直方向，C、D可看做重合。现有一可视为质点的小球从轨道ABC上距C点高为H的地方由静止释放。
（1）若要使小球经C处水平进入轨道DEF且能沿轨道运动，H至少要有多高?
（2）若小球静止释放处离C点的高度h小于（1）中H的最小值，小球可击中与圆心等高的E点，求此h的值。（取g=10m/s2）
如图所示为研究电子枪中电子在电场中运动的简化模型示意图。在Oxy平面的ABCD区域内，存在两个大小均为E的匀强电场I和II，两电场的边界均是边长为L的正方形（不计粒子所受重力，已知电子的质量为m，电量为e）。
（1）在该区域AB边的中点处由静止释放电子，电子离开匀强电场I的时间t和速率v0 。
（2）在该区域AB边的中点处由静止释放电
子，求电子离开ABCD区域的位置坐标；
（3）在电场I区域内适当位置由静止释放电子，电子恰能从ABCD区域左下角D处离开，求所有释放点的位置坐标；
如图所示，电源E恒定电压12V，定值电阻
，电动机M的内电阻为
，当开关s闭合，电动机转动稳定后，理想电压表的读数为
。若电动机除了内电阻外不计其他损耗。求:（1）电动机输出的机械功率P1.（2）电路消耗的总功率P。