尺规作图画线段AB的中垂线CD(E为垂足)时,为了方便起见,通常把四段弧的半径取成相等;其实不必如此,如图,若能确保弧①、②的半径相等(即AC=BC),再确保弧③、④的半径相等(即AD=BD),直线CD同样是线段AB的中垂线.请你给出证明.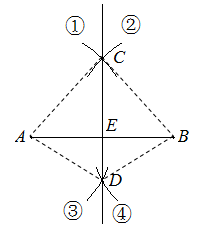
已知:如图,抛物线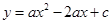 (
(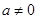 )与
)与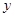 轴交于点
轴交于点 ( 0,4) ,与
( 0,4) ,与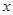 轴交于点
轴交于点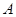 ,
,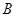 ,点
,点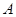 的坐标为(4,0).
的坐标为(4,0).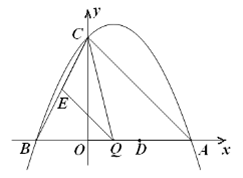
(1) 求该抛物线的解析式;
(2) 点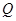 是线段
是线段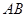 上的动点,过点
上的动点,过点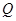 作
作 ∥
∥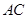 ,交
,交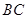 于点
于点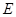 ,连接
,连接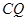 . 当
. 当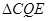 的面积最大时,求点
的面积最大时,求点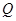 的坐标;
的坐标;
(3)若平行于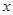 轴的动直线与该抛物线交于点
轴的动直线与该抛物线交于点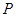 ,与直线
,与直线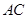 交于点
交于点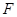 ,点
,点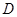 的坐标为(2,0). 问: 是否存在这样的直线,使得
的坐标为(2,0). 问: 是否存在这样的直线,使得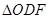 是等腰三角形?若存在,请求出点
是等腰三角形?若存在,请求出点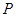 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
如图,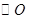 的直径
的直径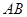 为10cm,弦
为10cm,弦 为6cm,
为6cm, 的平分线交
的平分线交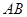 于
于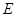 ,交
,交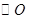 于
于 .求弦
.求弦 的长及
的长及 的值.
的值.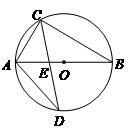
已知关于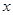 的方程
的方程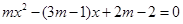
(1)求证:无论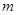 取任何实数时,方程恒有实数根;
取任何实数时,方程恒有实数根;
(2)若关于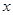 的二次函数
的二次函数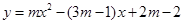 的图象与
的图象与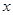 轴两交点间的距离为2时,求抛物线的解析式.
轴两交点间的距离为2时,求抛物线的解析式.
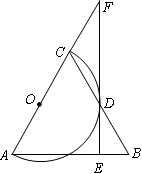
如图,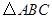 是等腰三角形,
是等腰三角形,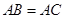 ,以
,以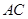 为直径的
为直径的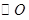 与
与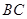 交于点
交于点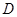 ,
,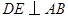 ,垂足为
,垂足为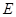 ,
,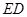 的延长线与
的延长线与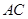 的延长线交于点
的延长线交于点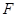 .
.
(1)求证: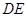 是
是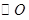 的切线;
的切线;
(2)若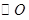 的半径为2,
的半径为2,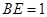 ,求
,求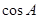 的值.
的值.
在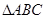 中,
中,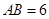 cm ,
cm ,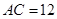 cm ,动点
cm ,动点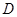 以1cm/s 的速度从点
以1cm/s 的速度从点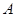 出发到点
出发到点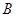 止,动点
止,动点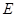 以2cm/s 的速度从点
以2cm/s 的速度从点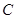 出发到点
出发到点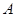 止,且两点同时运动,当以点
止,且两点同时运动,当以点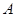 、
、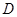 、
、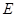 为顶点的三角形与
为顶点的三角形与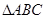 相似时,求运动的时间.
相似时,求运动的时间.