已知函数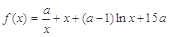 ,
, ,其中
,其中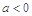 且
且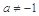 .
.
(Ⅰ) 当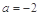 ,求函数
,求函数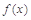 的单调递增区间;
的单调递增区间;
(Ⅱ)若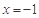 时,函数
时,函数 有极值,求函数
有极值,求函数 图象的对称中心的坐标;
图象的对称中心的坐标;
(Ⅲ)设函数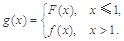 (
(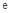 是自然对数的底数),是否存在a使
是自然对数的底数),是否存在a使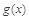 在
在 上为减函数,若存在,求实数a的范围;若不存在,请说明理由.
上为减函数,若存在,求实数a的范围;若不存在,请说明理由.
已知α,β都是锐角,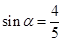 ,
,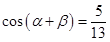 ,
, 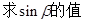 .
.
(1)化简: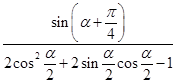 ;
;
(2)若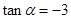 ,求
,求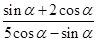 的值.
的值.
某厂生产一种仪器,由于受生产能力与技术水平的限制,会产生一些次品.根据经验知道,该厂生产这种仪器,次品率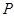 与日产量
与日产量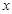 (件)(
(件)(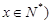 之间大体满足如框图所示的关系(注:次品率
之间大体满足如框图所示的关系(注:次品率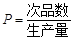 ).又已知每生产一件合格的仪器可以盈利
).又已知每生产一件合格的仪器可以盈利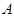 (元),但每生产一件次品将亏损
(元),但每生产一件次品将亏损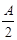 (元).(其中c为小于96的常数)
(元).(其中c为小于96的常数)
(1)若c=50,当x="46" 时,求次品率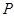 ;
;
(2)求日盈利额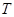 (元)与日产量
(元)与日产量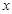 (件)(
(件)(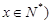 的函数关系;
的函数关系;
(3)当日产量为多少时,可获得最大利润?
已知数列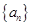 的前三项分别为
的前三项分别为 ,
, ,
,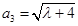 ,(其中
,(其中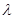 为正常数)。设
为正常数)。设
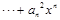 。
。
(1)归纳出数列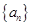 的通项公式,并证明数列
的通项公式,并证明数列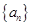 不可能为等比数列;
不可能为等比数列;
(2)若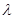 =1,求
=1,求 的值;
的值;
(3)若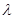 =4,试证明:当
=4,试证明:当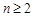 时,
时, .
.
我校为了了解高二级学生参加体育活动的情况,随机抽取了100名高二级学生进行调查.下面是根据调查结果绘制的学生日均参加体育活动时间的频率分布直方图: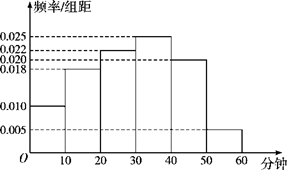
将日均参加体育活动时间不低于40分钟的学生称为参加体育活动的“积极分子”.根据已知条件完成下面的列联表,并据此资料,在犯错误的概率不超过5%的前提下,你是否认为参加体育活动的“积极分子”与性别有关?
| 非积极分子 |
积极分子 |
合计 |
|
| 男 |
15 |
45 |
|
| 女 |
|||
| 合计 |