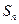已知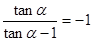 ,求下列各式的值:
,求下列各式的值:
(Ⅰ)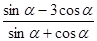 ;
;
(Ⅱ)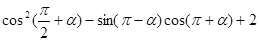 .
.
(本小题满分12分)
设函数f(x)=lnx,g(x)=ax+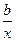 ,函数f(x)的图像与x轴的交点也在函数g(x)的图像上,且在此点处f(x)与g(x)有公切线.
,函数f(x)的图像与x轴的交点也在函数g(x)的图像上,且在此点处f(x)与g(x)有公切线.
(Ⅰ) 求a、b的值;
(Ⅱ) 设x>0,试比较f(x)与g(x)的大小.
(本小题满分12分)
如图5,平面ABDE⊥平面ABC,AC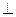 BC,AC=BC=4,四边形ABDE是直角梯形,BD
BC,AC=BC=4,四边形ABDE是直角梯形,BD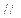 AE,BD
AE,BD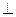 BA,AE=2BD=4,O、M分别为CE、AB的中点.
BA,AE=2BD=4,O、M分别为CE、AB的中点.
(Ⅰ) 证明:OD//平面ABC;
(Ⅱ)能否在EM上找一点N,使得ON⊥平面ABDE?
若能,请指出点N的位置,并加以证明;
若不能,请说明理由.
(本小题满分12分)
为了了解某市工人开展体育活动的情况,拟采用分层抽样的方法从A,B,C三个区中抽取7个工厂进行调查,已知A,B,C区中分别有18,27,18个工厂.
(Ⅰ)求从A,B,C区中分别抽取的工厂个数;
(Ⅱ)若从抽取的7个工厂中随机抽取2个进行调查结果的对比,计算这2个工厂中至少有1个来自A区的概率.
(本小题满分12分)
已知函数f(x)=x2-ax+b (a,b∈R)的图像经过坐标原点,且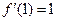 ,数列{
,数列{ }的前n项和
}的前n项和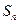 =f(n)(n∈N*).
=f(n)(n∈N*).
(Ⅰ) 求数列{ }的通项公式;(Ⅱ)若数列{
}的通项公式;(Ⅱ)若数列{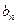 }满足
}满足 +
+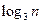 =
=  ,求数列{
,求数列{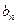 }的前n项和.
}的前n项和.
、已知数列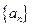 的前
的前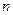 项和为
项和为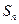 ,且
,且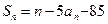 ,
,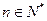
(1)求数列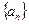 的通项公式
的通项公式
(2)求