(本题满分13分) 已知函数 ,数列
,数列 满足
满足 ,
, .
.
(Ⅰ)求数列 的通项公式
的通项公式 ;
;
(Ⅱ)求 ;
;
(Ⅲ)求证:
(本题满分13分) 已知函数 ,
, .
.
(1)当 时,若
时,若 上单调递减,求a的取值范围;
上单调递减,求a的取值范围;
(2)求满足下列条件的所有整数对 :存在
:存在 ,使得
,使得 的最大值,
的最大值, 的最小值;
的最小值;
(本题满分13分已知数列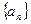 是公比为
是公比为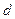
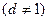 的等比数列,且
的等比数列,且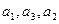 成等差数列.
成等差数列.
(Ⅰ) 求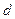 的值;
的值;
(Ⅱ) 设数列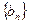 是以2为首项,
是以2为首项,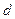 为公差的等差数列,其前
为公差的等差数列,其前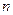 项和为
项和为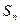 ,
,
试比较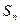 与
与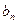 的大小.
的大小.
(本题满分13分)已知函数 满足
满足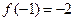 且对于任意
且对于任意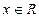 , 恒有
, 恒有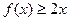 成立. (1) 求实数
成立. (1) 求实数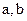 的值; (2) 解不等式
的值; (2) 解不等式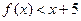 .
.
(本小题满分12分) (Ⅰ)小问7分,(Ⅱ)小问5分.)
已知O为坐标原点,向量=(sinα,1),=(cosα,0),=(-sinα,2),点P是直线AB上的一点,且点B分有向线段的比为1.
(1)记函数f(α)=·,α∈,讨论函数f(α)的单调性,并求其值域;
(2)若O、P、C三点共线,求|+|的值.