已知函数 ,其中a>0.
,其中a>0.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)若直线 是曲线
是曲线 的切线,求实数a的值;
的切线,求实数a的值;
(Ⅲ)设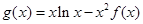 ,求
,求 在区间
在区间 上的最大值(其中e为自然对的底数)。
上的最大值(其中e为自然对的底数)。
(本小题满分12分)
已知直线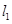 :
: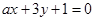 ,
, :
: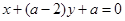 .
.
(1)若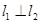 ,求实数
,求实数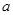 的值;
的值;
(2)当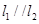 时,求直线
时,求直线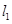 与
与 之间的距离.
之间的距离.
(本小题满分11分)
如图示,给出的是某几何体的三视图,其中正视图与侧视图都是边长为2的正三角形,俯视图为半径等于1的圆.试求这个几何体的侧面积与体积.
已知函数 且
且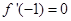
(Ⅰ)试用含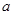 的代数式表示
的代数式表示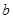 ;
;
(Ⅱ)求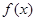 的单调区间;
的单调区间;
(Ⅲ)令 ,设函数
,设函数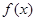 在
在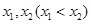 处取得极值,记点
处取得极值,记点 ,证明:线段
,证明:线段 与曲线
与曲线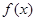 存在异于
存在异于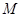 、
、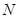 的公共点;
的公共点;
已知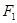
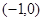 、
、
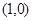 为椭圆的焦点,且直线
为椭圆的焦点,且直线 与椭圆相切.
与椭圆相切.
(Ⅰ)求椭圆方程;
(Ⅱ)过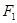 的直线交椭圆于
的直线交椭圆于 、
、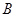 两点,求△
两点,求△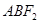 的面积
的面积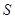 的最大值,并求此时直线的方程。
的最大值,并求此时直线的方程。
已知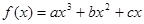 在区间[0,1]上是增函数,在区间
在区间[0,1]上是增函数,在区间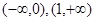 上是减函数,又
上是减函数,又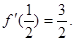
(Ⅰ)求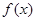 的解析式;
的解析式;
(Ⅱ)若在区间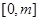 (m>0)上恒有
(m>0)上恒有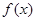 ≤
≤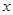 成立,求m的取值范围.
成立,求m的取值范围.