已知梯形ABCD中,AD∥BC,∠ABC =∠BAD =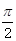 ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .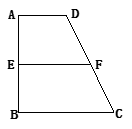
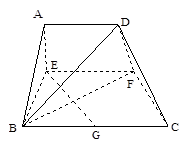
(1) 当x=2时,求证:BD⊥EG ;
(2) 若以F、B、C、D为顶点的三棱锥的体积记为f(x),求f(x)的最大值;
(3) 当f(x)取得最大值时,求二面角D-BF-C的余弦值.
某工厂计划生产甲、乙两种产品,这两种产品都需要两种原料。生产甲产品1工时需要A种原料3kg,B种原料1 kg;生产乙产品1工时需要A种原料2kg,B种原料2kg。现有A种原料1200 kg,B种原料800 kg。如果生产甲产品每工时的平均利润是30元,生产乙产品每工时的平均利润是40元,问甲、乙两种产品各生产多少工时能使利润的总额最大?最大利润是多少?
在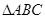 中内角
中内角 的对边分别为
的对边分别为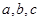 ,且
,且 ,
,
(1)求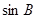 的值;
的值;
(2)如果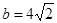 ,且
,且 ,求
,求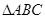 的面积.
的面积.
已知 ,解关于
,解关于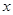 的不等式
的不等式 <
<
设
(1)求函数 的解析式.
的解析式.
(2)已知常数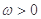 , 若
, 若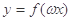 在区间
在区间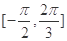 上是增函数,求
上是增函数,求 的取值范围.
的取值范围.
(3)设集合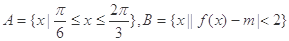 ,若
,若 ,求实数
,求实数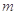 的取值范围.
的取值范围.
已知向量 且
且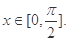 求:
求:
(1)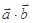 及
及
(2)若函数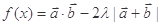 的最小值为
的最小值为 求实数
求实数 的值。
的值。