甲、乙两人各进行3次射击,甲每次击中目标的概率为 ,乙每次击中目标的概率为
,乙每次击中目标的概率为
求:(1)乙至少击中目标2次的概率;
(2)乙恰好比甲多击中目标2次的概率
某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
| 一次购物量 |
1至4件 |
5至8件 |
9至12件 |
13至16件 |
17件及以上 |
| 顾客数(人) |
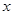 |
30 |
25 |
 |
10 |
| 结算时间(分钟/人) |
1 |
1.5 |
2 |
2.5 |
3 |
已知这100位顾客中的一次购物量超过8件的顾客占55%.
(Ⅰ)确定x,y的值,并求顾客一次购物的结算时间X的分布列与数学期望;
(Ⅱ)若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过2.5分钟的概率.(注:将频率视为概率)
某果园要用三辆汽车将一批水果从所在城市E运至销售城市F,已知从城市E到城市F有两条公路.统计表明:汽车走公路Ⅰ堵车的概率为 ,不堵车的概率为
,不堵车的概率为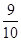 ;走公路Ⅱ堵车的概率为
;走公路Ⅱ堵车的概率为 ,不堵车的概率为
,不堵车的概率为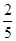 ,若甲、乙两辆汽车走公路Ⅰ,第三辆汽车丙由于其他原因走公路Ⅱ运送水果,且三辆汽车是否堵车相互之间没有影响.
,若甲、乙两辆汽车走公路Ⅰ,第三辆汽车丙由于其他原因走公路Ⅱ运送水果,且三辆汽车是否堵车相互之间没有影响.
(1)求甲、乙两辆汽车中恰有一辆堵车的概率;
(2)求三辆汽车中至少有两辆堵车的概率.
已知曲线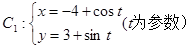 (t为参数),
(t为参数),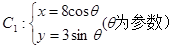
(1)化C ,C
,C 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若C 上的点P对应的参数为
上的点P对应的参数为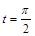 ,Q为C
,Q为C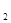 上的动点,求
上的动点,求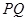 中点
中点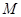 到直线
到直线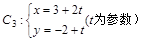 (t为参数)距离的最小值。
(t为参数)距离的最小值。
在极坐标中,已知圆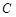 经过点
经过点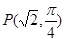 ,圆心为直线
,圆心为直线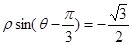 与极轴的交点,求圆
与极轴的交点,求圆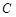 的极坐标方程.
的极坐标方程.