设椭圆
： 
的离心率为
，点
（
，0），
（0，
）原点
到直线
的距离为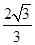
。
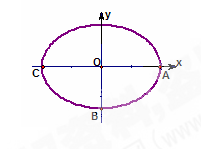
(1) 求椭圆的方程；
(2) 设点
为（
，0），点
在椭圆上（与、均不重合），点
在直线
上，若直线
的方程为
，且
，试求直线
的方程．
若等差数列
的前
项和为
，且满足
为常数，则称该数列为
数列．
（1）判断
是否为数列？并说明理由；
（2）若首项为
且公差不为零的等差数列为数列，试求出该数列的通项公式；
（3）若首项为，公差不为零且各项为正数的等差数列为数列，正整数
满足
，求
的最小值
已知函数
，当
时，
；
当
时，
．
（1）求
在
内的值域；
（2）
为何值时，
的解集为
．
如图, 在直三棱柱
中，
，
,
．
（1）求证：
；
（2）问：是否在
线段上存在一点
，使得
平面
？
若存在，请证明；若不存在，请说明理由。
已知数列
为等差数列，公差
，
是数列的前
项和, 且
.
（1）求数列的通项公式
；（2）令
，求数列
的前项和
.
在
中，内角
对边的边长分别是
，已知
，
,
，求的面积．