抛掷两颗质地均匀的骰子,计算:
(1)事件“两颗骰子点数相同”的概率;
(2)事件“点数之和小于7”的概率;
(3)事件“点数之和等于或大于11”的概率。
如图,半径为30 的圆形(
的圆形( 为圆心)铁皮上截取一块矩形材料
为圆心)铁皮上截取一块矩形材料 ,其中点
,其中点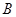 在圆弧上,点
在圆弧上,点 在两半径上,现将此矩形材料卷成一个以
在两半径上,现将此矩形材料卷成一个以 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设 与矩形材料的边
与矩形材料的边 的夹角为
的夹角为 ,圆柱的体积为
,圆柱的体积为
 .
.
(Ⅰ)求 关于
关于 的函数关系式?
的函数关系式?
(Ⅱ)求圆柱形罐子体积 的最大值.
的最大值.
已知函数 .
.
(Ⅰ)若曲线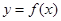 在点
在点 处的切线与直线
处的切线与直线 平行,求实数
平行,求实数 的值;
的值;
(Ⅱ)若函数 在
在 处取得极小值,且
处取得极小值,且 ,求实数
,求实数 的取值范围.
的取值范围.
已知函数 ,钝角
,钝角 (角
(角 对边为
对边为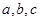 )的角
)的角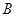 满足
满足 .
.
(Ⅰ)求函数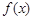 的单调递增区间;
的单调递增区间;
(Ⅱ)若 ,求
,求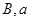 .
.
已知数列 的前
的前 项和为
项和为 满足
满足 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)求数列 的前
的前 项和
项和 .
.
如图,在四棱锥 中,底面
中,底面 为直角梯形,且
为直角梯形,且 ,
, ,平面
,平面 底面
底面 ,
, 为
为 的中点,
的中点, 是棱
是棱 的中点,
的中点, .
.

(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求三棱锥 的体积.
的体积.