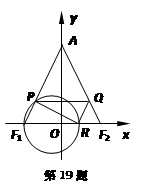设 是数列
是数列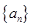 的前
的前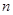 项和,对任意
项和,对任意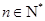 都有
都有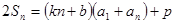 成立, (其中
成立, (其中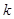 、
、 、
、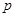 是常数).
是常数).
(1)当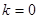 ,
,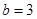 ,
,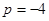 时,求
时,求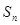 ;
;
(2)当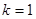 ,
,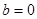 ,
,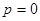 时,
时,
①若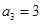 ,
,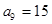 ,求数列
,求数列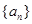 的通项公式;
的通项公式;
②设数列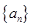 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“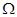 数列”.
数列”.
如果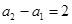 ,试问:是否存在数列
,试问:是否存在数列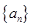 为“
为“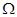 数列”,使得对任意
数列”,使得对任意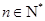 ,都有
,都有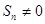 ,且
,且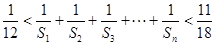 .若存在,求数列
.若存在,求数列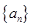 的首项
的首项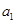 的所
的所
有取值构成的集合;若不存在,说明理由.
选修4﹣2:矩阵与变换
已知二阶矩阵 对应的变换将点(﹣2,1)变换成点(0,b),求实数a,b的值.
对应的变换将点(﹣2,1)变换成点(0,b),求实数a,b的值.
【选做题】本题包括A,B,C,D四小题,请选定其中两题作答,每小题10分,共计20分,解答时应写出文字说明,证明过程或演算步骤.
A.选修4—1:几何证明选讲
自圆O外一点P引圆的一条切线PA,切点为A,M为PA的中点,
过点M引圆O的割线交该圆于B、C两点,且∠BMP=100°,
∠BPC=40°,求∠MPB的大小.
(本小题满分16分)
已知函数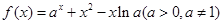 .
.
(Ⅰ)当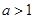 时,求证:函数
时,求证:函数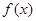 在
在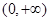 上单调递增;
上单调递增;
(Ⅱ)若函数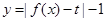 有三个零点,求
有三个零点,求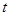 的值;
的值;
(Ⅲ)若存在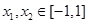 ,使得
,使得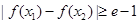 ,试求
,试求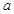 的取值范围.
的取值范围.
已知椭圆C:+=1(a>b>0)的离心率为,且经过点P(1,)。
(1)求椭圆C的方程;
(2)设F是椭圆C的右焦点,M为椭圆上一点,以M为圆心,MF为半径作圆M。问点M满足什么条件时,圆M与y轴有两个交点?
(3)设圆M与y轴交于D、E两点,求点D、E距离的最大值。
(本小题满分16分)如图,在平面直角坐标系 中,已知
中,已知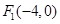 ,
, ,
,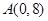 ,直线
,直线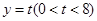 与线段
与线段 、
、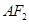 分别交于点
分别交于点 、
、 .
.
(Ⅰ)当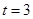 时,求以
时,求以 为焦点,且过
为焦点,且过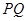 中点的椭圆的标准方程;
中点的椭圆的标准方程;
(Ⅱ)过点 作直线
作直线 ∥
∥ 交
交 于点
于点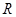 ,记
,记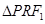 的外接圆为圆
的外接圆为圆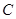 .
.
①求证:圆心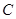 在定直线
在定直线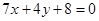 上;
上;
②圆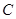 是否恒过异于点
是否恒过异于点 的一个定点?若过,求出该点的坐标;若不过,请说明理由.
的一个定点?若过,求出该点的坐标;若不过,请说明理由.