如图,三棱锥P—ABC中,PC⊥平面ABC,PC=AC=2,AB=BC, D是PB上一点,且CD⊥平面PAB.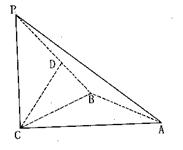
(1)求证:AB⊥平面PCB;
(2)求异面直线AP与BC所成角的大小;
已知 是抛物线
是抛物线 上的点,
上的点, 是
是 的焦点, 以
的焦点, 以 为直径的圆
为直径的圆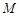 与
与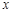 轴的另一个交点为
轴的另一个交点为 .
.
(Ⅰ)求 与
与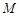 的方程;
的方程;
(Ⅱ)过点 且斜率大于零的直线
且斜率大于零的直线 与抛物线
与抛物线 交于
交于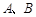 两点,
两点, 为坐标原点,
为坐标原点, 的面积为
的面积为 ,证明:直线
,证明:直线 与圆
与圆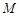 相切.
相切.
如图,在四棱锥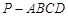 中,
中, 为平行四边形,且
为平行四边形,且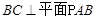 ,
,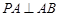 ,
,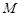 为
为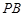 的中点,
的中点,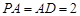 ,
,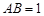 .
.
(Ⅰ)求证: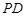 //
//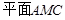 ;
;
(Ⅱ)求三棱锥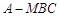 的高.
的高.
气象部门提供了某地今年六月份(30天)的日最高气温的统计表如下:
| 日最高气温t (单位:℃) |
t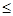 22℃ 22℃ |
22℃< t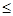 28℃ 28℃ |
28℃< t 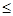 32℃ 32℃ |
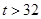 ℃ ℃ |
| 天数 |
6 |
12 |
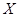 |
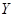 |
由于工作疏忽,统计表被墨水污染,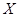 和
和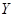 数据不清楚,但气象部门提供的资料显示,六月份的日最高气温不高于32℃的频率为0.9.
数据不清楚,但气象部门提供的资料显示,六月份的日最高气温不高于32℃的频率为0.9.
(Ⅰ) 若把频率看作概率,求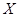 ,
,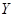 的值;
的值;
(Ⅱ) 把日最高气温高于32℃称为本地区的 “高温天气”,根据已知条件完成下面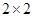 列联表,并据此你是否有95%的把握认为本地区的“高温天气”与西瓜“旺销”有关?说明理由.
列联表,并据此你是否有95%的把握认为本地区的“高温天气”与西瓜“旺销”有关?说明理由.
| 高温天气 |
非高温天气 |
合计 |
|
| 旺销 |
1 |
||
| 不旺销 |
6 |
||
| 合计 |
附: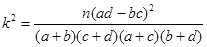
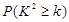 |
0.10 |
0.050 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
已知各项为正数的等差数列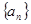 满足
满足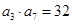 ,
,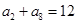 ,且
,且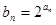 (
(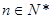 ).
).
(Ⅰ)求数列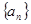 的通项公式;
的通项公式;
(Ⅱ)设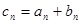 ,求数列
,求数列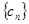 的前n项和
的前n项和 .
.
设函数 .
.
(Ⅰ)当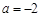 时,解不等式
时,解不等式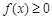 ;
;
(Ⅱ)当 时,不等式
时,不等式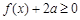 的解集为
的解集为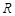 ,求实数
,求实数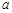 的取值范围.
的取值范围.