在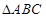 中,角
中,角 所对的边分别为
所对的边分别为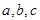 ,
, 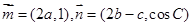 ,且
,且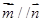 .求:
.求:
(1)求角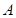 的值;
的值;
(2)求 的取值范围.
的取值范围.
已知函数f(x)=(x2+ax-2a2+3a)ex(x∈R),其中a∈R.
(1)当a=0时,求曲线y=f(x)在点(1,f(1))处的切线的斜率;
(2)当a≠ 时,求函数f(x)的单调区间与极值.
时,求函数f(x)的单调区间与极值.
设函数f(x)=a2ln x-x2+ax,a>0.
①求f(x)的单调区间;②求所有实数a,使e-1≤f(x)≤e2对x∈[1,e]恒成立.
一物体做变速直线运动,其v-t曲线如图所示,求该物体在 s~6 s间的运动路程.
s~6 s间的运动路程.
设y=f(x)是二次函数,方程f(x)=0有两个相等的实
根,且f′(x)=2x+2.
(1)求y=f(x)的表达式;
(2)求y=f(x)的图象与两坐标轴所围成图形的面积.
已知函数f(x)=x3-3ax2+2bx在点x=1处有极小值-1.
(1)求a、b;
(2)求f(x)的单调区间.