(本小题满分12分)已知椭圆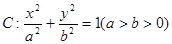 的离心率为
的离心率为 ,
, 在椭圆C上,A,B为椭圆C的左、右顶点.
在椭圆C上,A,B为椭圆C的左、右顶点.
(1)求椭圆C的方程:
(2)若P是椭圆上异于A,B的动点,连结AP,PB并延长,分别与右准线 相交于M1,M2.问是否存在x轴上定点D,使得以M1M2为直径的圆恒过点D?若存在,求点D的坐标:若不存在,说明理由.
相交于M1,M2.问是否存在x轴上定点D,使得以M1M2为直径的圆恒过点D?若存在,求点D的坐标:若不存在,说明理由.
(本小题满分12分)已知函数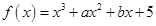 ,在
,在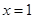 处取得极值且在点
处取得极值且在点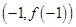 处的切线与
处的切线与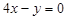 平行.
平行.
(1)求函数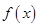 的解析式;
的解析式;
(2)当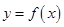 在
在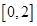 上的最小值和最大值;
上的最小值和最大值;
(3)若方程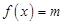 在
在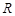 上有三个不同实根,求实数
上有三个不同实根,求实数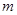 的取值范围.
的取值范围.
(本小题满分12分)在某次质量抽测后一数学老师随机抽取了30位(其中男、女各15名)学生的成绩,得出如下表,假设80分为“优秀”,否则为“不优秀”.
| 性别 |
成绩 |
| 男 |
83 81 96 68 83 77 86 97 78 64 85 91 90 99 82 |
| 女 |
74 70 68 86 92 72 76 78 78 64 86 66 79 68 70 |
(1)根据以上数据,试估计本次质量抽测数学科的优秀率(保留小数后三位);
(2)完成下列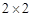 列联表:
列联表:
| 优秀 |
不优秀 |
合计 |
|
| 男 |
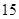 |
||
| 女 |
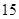 |
||
| 合计 |
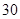 |
(3)利用分层抽样在“不优秀”的学生中抽取4人,再从抽取的4人随机抽取2人调查学习情况,求抽到一男一女的概率.
(本小题满分12分)如图等边三角形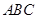 所在平面与菱形
所在平面与菱形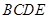 所在平面互相垂直,
所在平面互相垂直,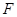 为
为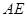 中点,
中点,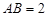 ,
,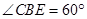 .
.
(1)求证: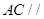 平面
平面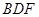 ;
;
(2)求点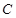 到平面
到平面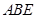 的距离.
的距离.
(本小题满分12分)在 中,内角
中,内角 ,
, ,
, 的对边分别为
的对边分别为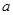 ,
,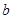 ,
, ,且
,且 .
.
(1)求角 的值;
的值;
(2)若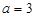 ,
, ,求
,求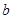 ,
, 的值.
的值.
(本小题满分12分)已知函数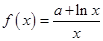 在
在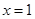 处取得极值.
处取得极值.
(1)求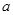 的值,并讨论函数
的值,并讨论函数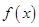 的单调性;
的单调性;
(2)当 时,
时,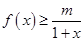 恒成立,求实数
恒成立,求实数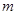 的取值范围.
的取值范围.