(本小题满分12分)已知函数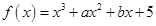 ,在
,在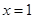 处取得极值且在点
处取得极值且在点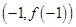 处的切线与
处的切线与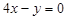 平行.
平行.
(1)求函数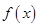 的解析式;
的解析式;
(2)当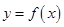 在
在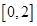 上的最小值和最大值;
上的最小值和最大值;
(3)若方程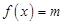 在
在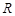 上有三个不同实根,求实数
上有三个不同实根,求实数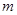 的取值范围.
的取值范围.
(本小题满分16分)
某厂生产一种仪器,由于受生产能力和技术水平的限制,会产生一些次品.根据经验知道,该厂生产这种仪器,次品率 与日产量
与日产量 (件)之间大体满足关系:
(件)之间大体满足关系:
(注:次品率 ,如
,如 表示每生产10件产品,约有1件为次品.其余为合格品.)
表示每生产10件产品,约有1件为次品.其余为合格品.)
已知每生产一件合格的仪器可以盈利 元,但每生产一件次品将亏损
元,但每生产一件次品将亏损 元,故厂方希望定出合适的日产量,
元,故厂方希望定出合适的日产量,
(1)试将生产这种仪器每天的盈利额 (元)表示为日产量
(元)表示为日产量 (件)的函数;
(件)的函数;
(2)当日产量 为多少时,可获得最大利润?
为多少时,可获得最大利润?
( 本小题满分14分)
本小题满分14分)
已知点 ,点
,点 是⊙
是⊙ :
: 上任意两个不同的点,且满足
上任意两个不同的点,且满足 ,设
,设 为弦
为弦 的中点.
的中点.
(1)求点 的轨迹
的轨迹 的方程;
的方程;
(2)试探究在轨迹 上是否存在这样的点:它到直线
上是否存在这样的点:它到直线 的距离恰好等于到点
的距离恰好等于到点 的距离?若存在,求出这样的点的坐标;若不存在,说明理由.
的距离?若存在,求出这样的点的坐标;若不存在,说明理由.
(本小题满分14分)
如图a,在直角梯形
 中,
中, ,
, 为
为 的中点,
的中点, 在
在 上,且
上,且 。已知
。已知 ,沿线段
,沿线段 把四边形
把四边形 折起如图b,使平面
折起如图b,使平面 ⊥平面
⊥平面 。
。
(1)求证: ⊥平面
⊥平面 ;
;
(2)求三棱锥 体积.
体积.
(本小题满分14分)
已知复数 ,
, ,(i为虚数单位,
,(i为虚数单位, ),且
),且 .
.
(1)若 且
且 ,求
,求 的值;
的值;
(2)设 ,已知当
,已知当 时,
时, ,试求
,试求 的值.
的值.
.(本小题满分14分)
已知函数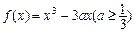 .
.
(1)当a=1时,求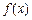 的极小值;
的极小值;
(2)设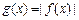 ,x∈[-1,1],求
,x∈[-1,1],求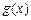 的最大值F(a).
的最大值F(a).