某租赁公司共有50台联合收割机，其中甲型20台，乙型30台．现将这50台联合收割机派往A、B两地收割小麦，其中30台派往A地，20台派往B地．两地区与该租赁公司商定的每天的租赁价格如下：
| |
甲型收割机的租金 |
乙型收割机的租金 |
| A地 |
1800元/台 |
1600元/台 |
| B地 |
1600元/台 |
1200元/台 |
（1）设派往A地x台乙型联合收割机，租赁公司这50台联合收割机一天获得的租金为y（元），请用x表示y，并注明x的范围．
（2）若使租赁公司这50台联合收割机一天获得的租金总额不低于79600元，说明有多少种分派方案，并将各种方案写出．
如图所示，在直角坐标平面内，函数的图象经过A(1，4)，B(a，b)，其中a>1．过点A作x轴垂线，垂足为C，过点B作y轴垂线，垂足为D，连结AD、DC、CB．
若△ABD的面积为4，求点B的坐标
求证：DC∥AB
四边形ABCD能否为菱形？如果能，请求出四边形ABCD 为菱形时，直线AB的函数解析式；如果不能，请说明理由．
某土产公司组织20辆汽车装运甲、乙、丙三种土特产共120吨去外地销售．按计划20辆车都要装运，每辆汽车只能装运同一种土特产，且必须装满．根据下表提供的信息，解答以下问题：
| 土特产种类 |
甲 |
乙 |
丙 |
| 每辆汽车运载量（吨） |
8 |
6 |
5 |
| 每吨土特产获利（百元） |
12 |
16 |
10 |
设装运甲种土特产的车辆数为
，装运乙种土特产的车辆数为
，求与之间的函数关系式如果装运每种土特产的车辆都不少于3辆，那么车辆的安排方案有几种？并写出每种安排方案．
若要使此次销售获利最大，应采用（2）中哪种安排方案？并求出最大利润的值
如图，BD为⊙O的直径，AB=AC，AD交BC于点E．
①求证：△ABE∽△ADB；②若AE=2，ED=4，求⊙O的面积
延长DB到F，使得，连接FA，若AC∥FD，试判断直线FA与⊙O的位置关系，并说明理由．
有3张扑克牌，分别是红桃3、红桃4和黑桃5．把牌洗匀后甲先抽取一张，记下花色和数字后将牌放回，洗匀后乙再抽取一张．先后两次抽得的数字分别记为s和t，则︱s－t︱≥1的概率
甲、乙两人做游戏，现有两种方案．A方案：若两次抽得相同花色则甲胜，否则乙胜．B方案：若两次抽得数字和为奇数则甲胜，否则乙胜．请问甲选择哪种方案胜率更高？
如图4，在梯形ABCD中，AD∥BC，AC⊥AB，AD=CD，cosB=
，BC=26．
求：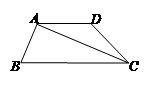
cos∠DAC的值；
线段AD的长