如图，在平面直角坐标系中，以点M（0，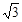
）为圆心，作⊙M交x轴于A、B两点，交y轴于C、D两点，连结AM并延长交⊙M于点P，连结PC交x轴于点E，连结DB，∠BDC=30°.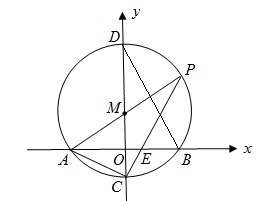
（1）求弦AB的长；
（2）求直线PC的函数解析式；
（3）连结AC，求△ACP的面积.
（1）探究归纳：如图，已知△ABC与△ABD的面积相等，试判断（1）AB与CD的位置关系，并说明理由．
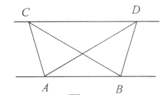
（2）结论应用：①如图，点M,N在反比例函数
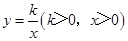的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，垂足分别为E，F．证明：MN∥EF．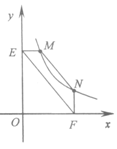
②如图，点M,N在反比例函数y=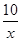
的图象上，且M（2,m）,N是第三象限内反比例函数y=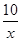的图象上一动点．过点M作ME⊥y轴，过点N作EF⊥x轴，垂足分别为E，F．说明MN∥EF．并求当四边形MEFN的面积为12时点N的坐标．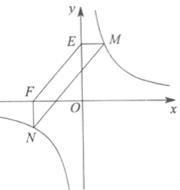
某工厂生产甲、乙两种产品，其中A车间只生产甲种产品，B车间只生产乙种产品．A车间每天生产的甲种产品数量比B车间每天生产的乙种产品数量少3件，B车间2天生产的乙种产品数量比A车间3天生产的甲种产品数量少1件．（1）求A车间每天生产多少甲种产品？B车间每天生产多少件乙种产品？
（2）该工厂生产的甲种产品的出厂价为每件160元，乙种产品的出厂价为每件210元．某客户需一次性购买甲、乙两种产品共100件，该工厂A、B两车间在没有库存的情况下，同时生产了7天，该客户按出厂价购买甲、乙两种产品的费用不少于18500元而少于18650元．请你通过计算为该客户设计购买方案．
如图，在
中，AC、BD交于点O，∠ABC=60°,AB=1,E、F分别是线段BO、DO上不与点O重合的点，且BE=DF．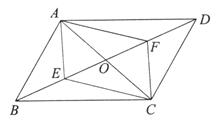
（1）探究：当BC的长为多少时，四边形AECF是菱形？并说明理由．
（2）当四边形AECF是正文形时，求DF的长．
如图，流经某市的一条河流的两岸互相平行，河岸l1上有一排观赏灯，已知相邻两灯之间的距离AB=60米，某人在河岸l2的C处测得∠ACE=60°,然后沿河岸向右走了140米到达D处，测得∠BDE=30°．求河流的宽度AE（结果保留三个有效数字，参考数据：
）．
如图，AB⊥EF，DC⊥EF，垂足分别为B、C,且AB=CD,BE=CF．AF、DE相交于点O，AF、DC相交于点N,DE、AB相交于点M．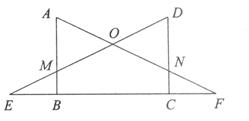
（1）请直接写出图中所有的等腰三角形；
（2）求征：△ABF≌△DCE．