已知函数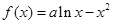 .
.
(1)当 时,求函数
时,求函数 在
在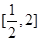 上的最大值;
上的最大值;
(2)令 ,若
,若 在区间
在区间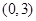 上不单调,求
上不单调,求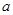 的取值范围;
的取值范围;
(3)当 时,函数
时,函数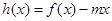 的图象与
的图象与 轴交于两点
轴交于两点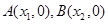 ,且
,且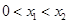 ,又
,又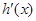 是
是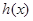 的导函数.若正常数
的导函数.若正常数 满足条件
满足条件 .证明:
.证明: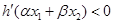 .
.
(本小题满分13分)已知向量 ,
, ,
, (a为常数),曲线y=f(x)在点(1,f(1))处的切线与y轴垂直.
(a为常数),曲线y=f(x)在点(1,f(1))处的切线与y轴垂直.
(1)求a的值及f(x)的单调区间;
(2)已知函数g(x)=-x2+2bx(b为常数),若对于任意的x2∈[0,1],总存在x1∈(0,+∞),使得g(x2)<f(x1),求b的取值范围.
(本小题满分12分)2013年2月20日,针对房价过高,国务院常务会议确定五条措施(简称“国五条”).为此,记者对某城市的工薪阶层关于“国五条”态度进行了调查,随机抽取了60人,作出了他们的月收入频率分布直方图(如图),同时得到了他们月收入情况与“国五条”赞成人数统计表(如下表):
(1)试根据频率分布直方图估计这60人的平均月收入;
(2)若从月收入(单位:百元)在[65,75)的被调查者中各随机选取2人进行追踪调查,求2人都不赞成的概率.
(本小题满分12分)如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD,AD∥BC,AD⊥CD,BC=ED=2AE,F为PC上一点,且CF=2FP.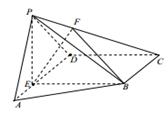
(1)求证:PA∥平面BEF;
(2)求三棱锥P-ABF与三棱锥F-EBC的体积之比.
(本小题满分12分)已知函数f(x)= sinxcosx-3cos2x+
sinxcosx-3cos2x+
(1)求函数f(x)的最小正周期及单调递增区间;
(2)△ABC的内角A,B,C的对边分别是a,b,c,若 ,b=1,c=
,b=1,c= ,且a>b,试判断△ABC的形状,并说明理由.
,且a>b,试判断△ABC的形状,并说明理由.
(本小题满分12分)已知等差数列{an}的前n项和为Sn,且a2=-5,S5=-20.
(1)求数列{an}的通项公式;
(2)求使得不等式Sn>an成立的n的最小值.