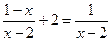为了探索代数式
的最小值，
小张巧妙的运用了数学思想．具体方法是这样的：如图，C为线段BD上一动点，分别过点B、D作
，连结AC、EC．已知AB=1，DE=5，BD=8，设BC=x．则
，
则问题即转化成求AC+CE的最小值．
(1)我们知道当A、C、E在同一直线上时，AC+CE的值最小，于是可求得的最小值等于 ，此时
；
(2)题中“小张巧妙的运用了数学思想”是指哪种主要的数学思想?
(选填：函数思想，分类讨论思想、类比思想、数形结合思想)
(3)请你根据上述的方法和结论，试构图求出代数式
的最小值.
欢欢有红色、白色、黄色三件上衣，又有米色、白色的两条裤子．
（1）她随机拿出一件上衣和一条裤子,用树状图(或列表法)表示所有可能出现的结果；
（2）如果欢欢最喜欢的穿着搭配是白色上衣配米色裤子，求欢欢随机拿出一件上衣和一条裤子正好是她最喜欢的穿着搭配的概率.
如图， F、C是线段AD上的两点，AB∥DE，BC∥EF
，AF=DC，
连结AE、BD，求证：四
边形ABDE是平行四边形。
如图2，正方形网格中，△ABC为格点三角形（顶点都是格
点），将△ABC绕点A按逆时针方向旋转90°得到
．
（1）在正方形网格中，作出；（不要求写作法）
（2）设网格小正方形的边长为1cm，求线段AB所扫过的图形的面积．（结果保留
）
先化简代数式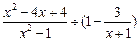
，然后选取一个合适的x
代入求值．
解方程: