已知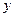 与
与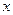 -3成反比例,且当
-3成反比例,且当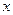 =4时,
=4时,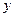 =5,求:
=5,求:
(1)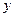 与
与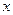 之间的函数关系式;
之间的函数关系式;
(2)当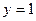 时,求
时,求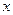 的值.
的值.
已知:如图,AB=3,AC=4,AB⊥AC,BD=12,CD=13,(1)求BC的长度;(2)证明:BC⊥BD.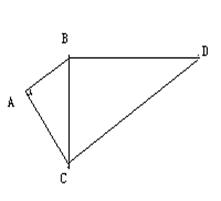
解分式方程: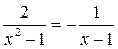
(8分)在甲村至乙村的公路有一块山地正在开发.现有一C处需要爆破.已知点C
与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,
如图13所示.为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公
路AB段是否有危险,是否需要暂时封锁? 请通过计算进行说明。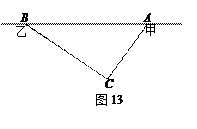
如图,正方形OABC的面积为9,点O为坐标原点,点B在函数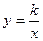
(k>0,x>0)的图象上,点P(m、n)是函数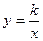 (k>0,x>0)的图象上任意一点,
(k>0,x>0)的图象上任意一点,
过点P分别作x轴、y轴的垂线,垂足分别为E、F,并设矩形OEPF和正方形OABC不重合部分的面积为S.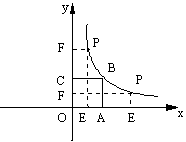
(1)求B点坐标和k的值;
(2)当S=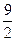 时,求点P的坐标。
时,求点P的坐标。