如图,AB为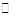 O的直径,射线AP交
O的直径,射线AP交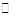 O于C点,∠PCO的平分线交
O于C点,∠PCO的平分线交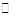 O于D点,过点D作
O于D点,过点D作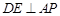 交AP于E点.
交AP于E点.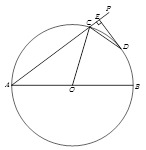
(1)求证:DE为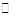 O的切线;
O的切线;
(2)若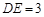 ,
,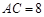 ,求直径
,求直径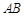 的长.
的长.
为了净化空气,美化环境,我县城兴华小区计划投资1.8万元种玉兰树和松柏树共80棵,已知某苗圃负责种活以上两种树苗的价格分别为:300元/棵,200元/棵,问可种玉兰树和松柏树各多少棵?
甲、乙两位同学在解方程组 时,甲看错了第一个方程,解得
时,甲看错了第一个方程,解得 ,乙看错了第二个方程,解得
,乙看错了第二个方程,解得 .求a、b的值.
.求a、b的值.
解方程组
(1) ;
;
(2) .
.
观察一列数:1、2、4、8、16、…我们发现,这一列数从第二项起,每一项与它前一项的比都等于2.一般地,如果一列数从第二项起,每一项与它前一项的比都等于同一个常数,这一列数就叫做等比数列,这个常数就叫做等比数列的公比.
(1)等比数列5、﹣15、45、…的第4项是 .
(2)如果一列数a1,a2,a3,a4是等比数列,且公比为q.那么有:a2=a1q,a3=a2q=(a1q)q=a1q2,a4=a3q=(a1q2)q=a1q3
则:a5= .(用a1与q的式子表示)
(3)一个等比数列的第2项是10,第4项是40,求它的公比.
统计数据显示,在我国的664座城市中,按水资源情况可分为三类:暂不缺水城市、一般缺水城市和严重缺水城市.其中,暂不缺水城市数比严重缺水城市数的3倍多52座,一般缺水城市数是严重缺水城市数的2倍.求严重缺水城市有多少座?