Rt△ABC与Rt△FED是两块全等的含30o、60o角的三角板，按如图（一）所示拼在一起，CB与DE重合．
（1）求证：四边形ABFC为平行四边形；
（2）取BC中点O，将△ABC绕点O顺时钟方向旋转到如图（二）中△
位置，直线
与AB、CF分别相交于P、Q两点，猜想OQ、OP长度的大小关系，并证明你的猜想．
(3)在(2)的条件下,指出当旋转角至少为多少度时,四边形PCQB为菱形(不要求证明).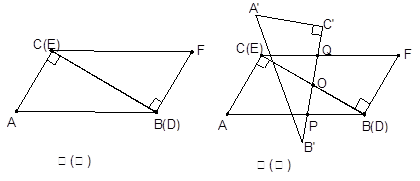
已知扇形的圆心角为240º，面积为
πcm2.
（1）求扇形的弧长；
（2）若把此扇形卷成一个圆锥，则这个圆锥的轴截面面积是多少？
某检修小组乘一辆汽车沿公路东西方向检修线路，约定向东为正，某天从A地出发到收工时行走记录为（单位：千米）：
+15、—2、+5、—1、—3、—2、+4、—5
（1）计算收工时，检修小组在A地的哪一边，距A地多远？
（2）若每千米汽车耗油量为0.4升，求出发到收工检修小组耗油多少升？
观察下列等式：
，
，
，
由此可知
1－
＋－
＋－
＝1－＝
.
（1）猜想并写出：
＝；
（2）计算：
＋…＋
计算：
（1）
；
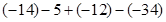（2）
；
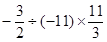（3）
；
（4）—99
×30（用简便方法计算）；
把下列各数填在相应的大括号里：
，22，
，
，0，
，—2012
整数：｛｝
正分数：｛｝
负有理数数：｛｝