已知圆
，直线
，以O为极点，x轴的正半轴为极轴，取相同的单位长度建立极坐标系.
（1）将圆C和直线
方程化为极坐标方程；
（2）P是上的点，射线OP交圆C于点R，又点Q在OP上且满足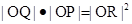
，当点P在上移动时，求点Q轨迹的极坐标方程.
（本题10分）已知函数
（1）判断函数
的单调性，并证明；
（2）求函数的最大值和最小值．
（本题10分）设
，
（1）在下列直角坐标系中画出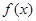
的图象；
（2）若
，求
值．
（本题10分）设全集为R，集合A＝{x|3≤x<6}，B＝{x|2<x<9}．
（1）分别求A∩B，（∁RB）∪A；
（2）已知C＝{x|a<x<a＋1}，若C⊆B，求实数a的取值范围构成的集合．
首项都是1的两个数列{an}，{bn}（bn≠0，n∈N*）满足an＋1bn－ anbn＋1＝2bn＋1bn．
（1）令cn＝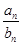
，求证：数列{cn}是等差数列；
（2）若bn＝3n－1，求数列{an}的前n项和Sn．
等差数列{an}的公差d为整数，已知a1＝10，且a4≥0，a5≤0，
（1）求{an}的通项公式；
（2）设bn＝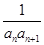
，求数列{bn}的前n项和Tn．