(本题10分)设全集为R,集合A={x|3≤x<6},B={x|2<x<9}.
(1)分别求A∩B,(∁RB)∪A;
(2)已知C={x|a<x<a+1},若C⊆B,求实数a的取值范围构成的集合.
某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得如图柱状图:

记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用(单位:元),n表示购机的同时购买的易损零件数.
(Ⅰ)若 ,求y与x的函数解析式;
(Ⅱ)若要求“需更换的易损零件数不大于n”的频率不小于0.5,求n的最小值;
(Ⅲ)假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件?
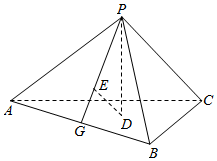
如图,已知正三棱锥 的侧面是直角三角形, ,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连接PE并延长交AB于点G.
(Ⅰ)证明:G是AB的中点;
(Ⅱ)在图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
设
,向量
,
,
,
.
(1)若
,求
;
(2)若
,求
的值;
(3)若
,求证:
.
已知
,
.
(1)求
的值;
(2)求
的值.
已知函数
在x=
时取得最大值4..
(1)求
的最小正周期;
(2)求
的解析式;
(3)若
.求
的值.