如图所示,直线 和圆 相切于点 ,交直径 的延长线于点 .过点 作 的垂线,交 于点 ,交圆 于点 .作平行四边形 ,连接 , , .
(1)求证: ;
(2)求 及 的大小.

某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车恰好全部坐满.已知每辆大客车的乘客座位数比小客车多17个.
(1)求每辆大客车和每辆小客车的乘客座位数;
(2)由于最后参加活动的人数增加了30人,学校决定调整租车方案.在保持租用车辆总数不变的情况下,为将所有参加活动的师生装载完成,求租用小客车数量的最大值.

为提高节水意识, 小申随机统计了自己家 7 天的用水量, 并分析了第 3 天的用水情况, 将得到的数据进行整理后, 绘制成如图所示的统计图 . (单 位: 升)
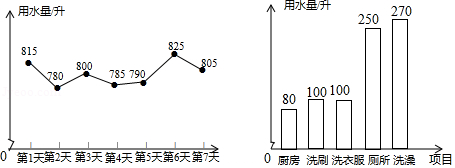
(1) 求这 7 天内小申家每天用水量的平均数和中位数;
(2) 求第 3 天小申家洗衣服的水占这一天总用水量的百分比;
(3) 请你根据统计图中的信息, 给小申家提出一条合理的节约用水建议, 并估算采用你的建议后小申家一个月 (按 30 天计算) 的节约用水量 .
如图所示,已知平行四边形 ,对角线 , 相交于点 , .
(1)求证:平行四边形 是矩形;
(2)请添加一个条件使矩形 为正方形.

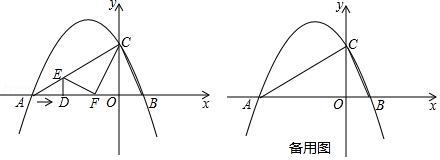
如图,抛物线 与 轴交于两点 和 ,与 轴交于点 ,动点 沿 的边 以每秒2个单位长度的速度由起点 向终点 运动,过点 作 轴的垂线,交 的另一边于点 ,将 沿 折叠,使点 落在点 处,设点 的运动时间为 秒.
(1)求抛物线的解析式和对称轴;
(2)是否存在某一时刻 ,使得 为直角三角形?若存在,求出 的值;若不存在,请说明理由;
(3)设四边形 的面积为 ,求 关于 的函数表达式.