将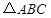 绕点
绕点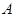 按逆时针方向旋转,旋转角为
按逆时针方向旋转,旋转角为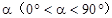 ,旋转后使各边长变为原来的
,旋转后使各边长变为原来的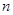 倍,得到
倍,得到 ,我们将这种变换记为[
,我们将这种变换记为[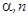 ].
].
(1)如图①,对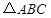 作变换[
作变换[ ]得
]得 ,则
,则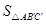 :
: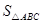 = ___;直线
= ___;直线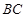 与直线
与直线 所夹的锐角为 __ °;
所夹的锐角为 __ °;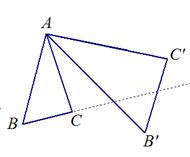
图①
(2)如图②,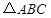 中,
中, ,对
,对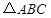 作变换[
作变换[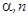 ]得
]得 ,使得四边形
,使得四边形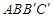 为梯形,其中
为梯形,其中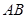 ∥
∥ ,且梯形
,且梯形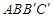 的面积为
的面积为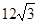 ,求
,求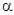 和
和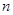 的值.
的值.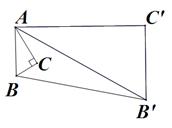
图②
阅读与思考
如图是小宇同学的数学日记,请仔细阅读,并完成相应的任务.
|
年 月 日星期日 没有直角尺也能作出直角 今天,我在书店一本书上看到下面材料:木工师傅有一块如图①所示的四边形木板,他已经在木板上画出一条裁割线 ,现根据木板的情况,要过 上的一点 ,作出 的垂线,用锯子进行裁割,然而手头没有直角尺,怎么办呢? 办法一:如图①,可利用一把有刻度的直尺在 上量出 ,然后分别以 , 为圆心,以 与 为半径画圆弧,两弧相交于点 ,作直线 ,则 必为 .
办法二:如图②,可以取一根笔直的木棒,用铅笔在木棒上点出 , 两点,然后把木棒斜放在木板上,使点 与点 重合,用铅笔在木板上将点 对应的位置标记为点 ,保持点 不动,将木棒绕点 旋转,使点 落在 上,在木板上将点 对应的位置标记为点 .然后将 延长,在延长线上截取线段 ,得到点 ,作直线 ,则 . 我有如下思考:以上两种办法依据的是什么数学原理呢?我还有什么办法不用直角尺也能作出垂线呢? |
任务:
(1)填空:“办法一”依据的一个数学定理是 ;
(2)根据“办法二”的操作过程,证明 ;
(3)①尺规作图:请在图③的木板上,过点 作出 的垂线(在木板上保留作图痕迹,不写作法);
②说明你的作法所依据的数学定理或基本事实(写出一个即可).
2020年国家提出并部署了“新基建”项目,主要包含“特高压,城际高速铁路和城市轨道交通, 基站建设,工业互联网,大数据中心,人工智能,新能源汽车充电桩”等.《2020新基建中高端人才市场就业吸引力报告》重点刻画了“新基建”中五大细分领域 基站建设,工业互联网,大数据中心,人工智能,新能源汽车充电桩)总体的人才与就业机会.如图是其中的一个统计图.

请根据图中信息,解答下列问题:
(1)填空:图中2020年“新基建”七大领域预计投资规模的中位数是 300 亿元;
(2)甲,乙两位待业人员,仅根据上面统计图中的数据,从五大细分领域中分别选择了“ 基站建设”和“人工智能”作为自己的就业方向.请简要说明他们选择就业方向的理由各是什么;
(3)小勇对“新基建”很感兴趣,他收集到了五大细分领域的图标,依次制成编号为
,
,
,
,
的五张卡片(除编号和内容外,其余完全相同),将这五张卡片背面朝上,洗匀放好,从中随机抽取一张(不放回),再从中随机抽取一张.请用列表或画状图的方法求抽到的两张卡片恰好是编号为
基站建设)和
(人工智能)的概率.
如图,四边形 是平行四边形,以点 为圆心, 为半径的 与 相切于点 ,与 相交于点 , 的延长线交 于点 ,连接 交 于点 .求 和 的度数.

2020年5月份,省城太原开展了“活力太原 乐购晋阳”消费暖心活动,本次活动中的家电消费券单笔交易满600元立减128元(每次只能使用一张).某品牌电饭煲按进价提高 后标价,若按标价的八折销售,某顾客购买该电饭煲时,使用一张家电消费券后,又付现金568元.求该电饭煲的进价.

(1)计算: .
(2)下面是小彬同学进行分式化简的过程,请认真阅读并完成相应任务.
第一步
第二步
第三步
第四步
第五步
第六步
任务一:填空:
①以上化简步骤中,第 步是进行分式的通分,通分的依据是 .或填为: ;
②第 步开始出现错误,这一步错误的原因是 ;
任务二:请直接写出该分式化简后的正确结果;
任务三:除纠正上述错误外,请你根据平时的学习经验,就分式化简时还需要注意的事项给其他同学提一条建议.